Settling Basins for Trickle Irrigation in Florida
Trickle irrigation systems deliver water, nutrients and other chemicals at low rates and high frequency directly to the root zone of the plant. Water is distributed through an extensive network of pipes and delivered in the form of drops, tiny streams, or miniature sprays by emitters. Well-managed trickle irrigation systems result in water and nutrient savings due to application of water into or near the root zone, and energy savings due to low operating pressure (compared to other pressurized irrigation methods). However, trickle irrigation systems usually require a higher level of management than other irrigation systems.
Water quality is a major concern in the management of trickle irrigation systems. The potential for the emitters to become plugged by physical, chemical or biological contaminants creates significant problems to be addressed in everyday maintenance. By far, the most common problem is blockage of the emitter passage by solid particles in the irrigation water (sand, plant debris, etc.). therefore, effective and reliable water treatment is mandatory for the successful operation of trickle irrigation systems.
Generally, groundwater requires less treatment and causes fewer clogging problems for trickle irrigation systems than surface water. However, groundwater containing high levels of iron and sulfur, which is often the case here in Florida, can cause bacterial growth and severe clogging problems if the water is not properly treated.
Often, the most economical source of irrigation water is from a river, canal, stream, or irrigation ditch. Water from these sources the greatest potential for clogging problems, due to the organic contaminants that are usually present. Nevertheless, if organic growth can be eliminated and all debris filtered out, surface water can be successfully used for trickle irrigation.
Settling Basins
Settling basins can provide an effective and economical solution for two water treatment problems: (1) high levels of turbulence (suspended particles of sand and silt) in surface waters, and (2) high levels of dissolved iron in groundwaters. A settling basin can serve as the primary filtration unit, increasing the efficiency of secondary filters in the irrigation system and decreasing the frequency of required filter cleanings.
However, settling basins should not be used unless one of these problems is present, since a basin can easily introduce other problems, particularly if the water supply is from a well. The basin can catch windblown contaminants, and algal growth in the pool may create greater filtration problems than those caused by sand and silt from the well. Frequent chemical treatment of the basin water and media filtration may be necessary to remove this organic contamination.
Settling basins can remove suspended inorganic particles ranging from sand (2 mm in diameter) to silt (0.002 mm in diameter), depending on basic design. The finer sediments require longer settling times and, hence, longer water transit times through the basin.
The size of the basin is a function of the flow rate of water that must be treated, the size of the sediments in the water, and the water quality required at the outlet. It is usually not practical to remove small silt and clay particles (smaller than 0.002 mm), unless they are flocculated using alum and/or polyelectrolites. Without chemical coagulation, the sedimentation time required is extremely long. These particles are small enough not to cause any problem, and chemical treatment may be too costly for an irrigation system.
For a trickle irrigation system, it is generally assumed that the smallest particles that need to be removed have equivalent diameters of 75 microns, which corresponds to 200-mesh filtration. Particles of this size can be satisfactorily removed in a well-designed settling basin. However, a screen filter at the entrance to the irrigation system is also recommended as a safety device to filter any debris picked up by the pump.
Sedimentation
Sedimentation is the removal of suspended particles that are heavier than water by gravitational settling. Where sedimentation employs only the natural force of gravity and natural particle aggregation, it is called plain sedimentation. Plain sedimentation includes two types of processes. One type is called free settling, a process by which relatively large particles such as sand and silt settle individually. This usually happens in suspensions with low concentrations of solids and where particles are large. The other type of settling is preceded by natural flocculation of the particles, which forms aggregated, larger particles that can settle faster due to their increased mass. An example of this type of sedimentation is the oxidation and flocculation of iron.
When chemicals or other substances are added to induce aggregation and settling of fine suspended particles, the process is called coagulation (5). The most common coagulants used are alum, sodium aluminate, ammonium alum, copperas (ferrous sulfate), ferric sulfate and pulverized limestone. Coagulation can be expensive and uneconomical for irrigation purposes.
Determination of Settling Velocity
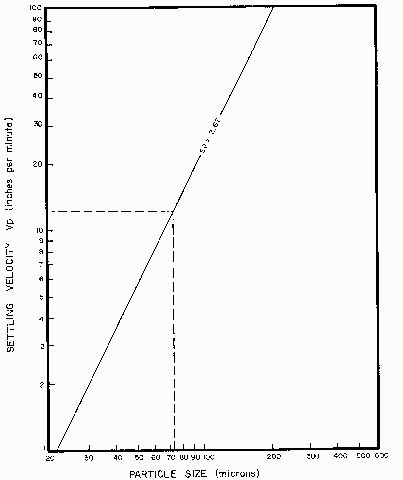
When discrete, nonflocculating particles such as sand and larger particles of silt are settling due to the force of gravity (free settling), sedimentation velocity can be determined from Stokes' law. The velocity of sedimentation depends upon particle size, shape and density. Settling velocity of spherical, smooth and rigid particle varies with the square of its diameter according to Equation 1: For inorganic soil particles, SG is typically taken as 2.6, the specific gravity of quartz. Equation 1 assumes that the settling particle is spherical, smooth and rigid, which is hardly true of typical soil particles. However, the concept of particle equivalent diameter allows use of Equation 1 to estimate the settling velocity of soil particles. A particle's equivalent diameter is the diameter of a sphere made from the same material, which would fall with the same velocity as the particle of interest. Frequently, a plate-shaped soil particle will be larger than its equivalent diameter. Figure 1 gives settling velocities for different particle sizes (equivalent diameter). From this graph it can be found that the settling velocity for 75-micron particles is 12.7 inches per minute. Note, however, that the actual size of 75-micron equivalent diameter particles may be larger than 75 microns.

Where natural flocculation occurs, the settling velocity of the aggregated particles must be measured in a settling column under laboratory conditions before a settling basins can be designed. It is difficult to estimate this velocity theoretically, since the extent of flocculation depends on empirical factors such as particle shape and surface geometry, the range of particle sizes present in the water, velocity gradients in the system, and the depth of the basin.
The height of the laboratory settling column should be equal to the depth of the proposed settling basin, since the depth of the basin will influence the extent of flocculation and, as a result, the settling time. The diameter of the settling column does not influence settling velocity, so a column of any diameter can be used. It is important that at the beginning of the experiment the number and sizes of suspended particles are uniformly distributed from the top to the bottom of the column. The particle settling velocity is calculated by dividing the settling distance by the time required to obtain clean water in the column.
Settling Basin Design
The first step in the design of a settling basin is to decide what size particles should be removed from the irrigation water to prevent the emitters from clogging. Assuming that Stokes' law holds for the suspended material, the settling velocity of the chosen particle can be easily determined from Equation 1.
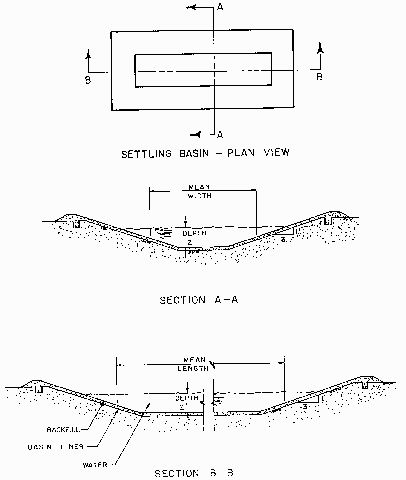
The surface area required for a settling basin is determined from the calculated settling velocity and the water inflow rate, or according to Equation 2: The settling basin length should be approximately five times its width. Where construction area is limited, a U-shape design may be recommended. If cross sections of the settling basin are trapezoidal, the mean width and mean length should be considered in the design (Figure 2). Whenever the basin length (L) equals five times the width (W), they may each be determined from the area as shown in Equation 3: The time required for a unit of water to flow through the settling basin is called the detention time. This time should be long enough so that all particles of the chosen size will settle at the bottom of the basin. The basin depth (D) and detention time (t) are related to the design settling velocity of the chosen particle size (Vp, which can be determined from Equation 1) according to Equation 4: It is the ratio of basin depth to detention time that is important, not just basin depth or detention time alone. Theoretically, as long as the ratio of basin depth to detention time is less than or equal to the settling velocity, the basin will operate properly. Sizing the basin according to equation (2) or equation (4) will ensure that this condition is met. In practice, the minimum required detention time for the particles to be removed for irrigation purposes is so short, that the basin depth can be selected to suit topography or other convenience considerations.

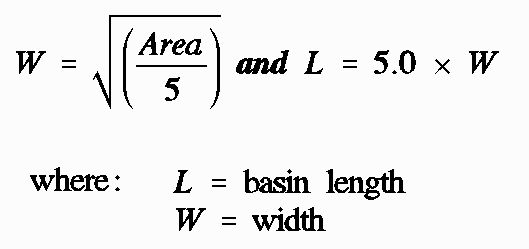
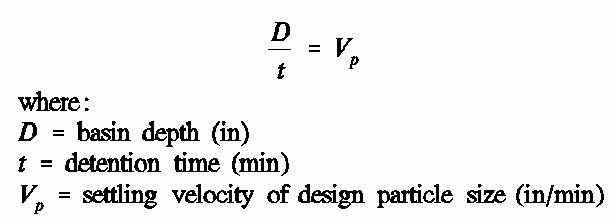
As sediment accumulates on the bottom of the basin, the depth decreases. Therefore, an allowance must be made for sediment storage in the design. The minimum amount of storage required will depend on how much sediment is carried by the water and on how often the basin is cleaned. Storage and other factors - such as turbulence at the inlet to and from the outlet to the basin, and differences in velocities of water in various parts of the basin - are usually included in the storage factor F (safety factor), which results in the overdesign of the basin to make sure that the desired particles will be removed. A value of F = 2 is often used. With this safety factor, Equation 2 will have the form as shown in Equation 5:

Basin Inlet and Outlet
The inlet to a settling basin should minimize entrance velocities, create very little turbulence, and distribute water across the basin as uniformly as possible. Diffusion structures or baffles (Figure 3) are usually used for this purpose at the entrance.
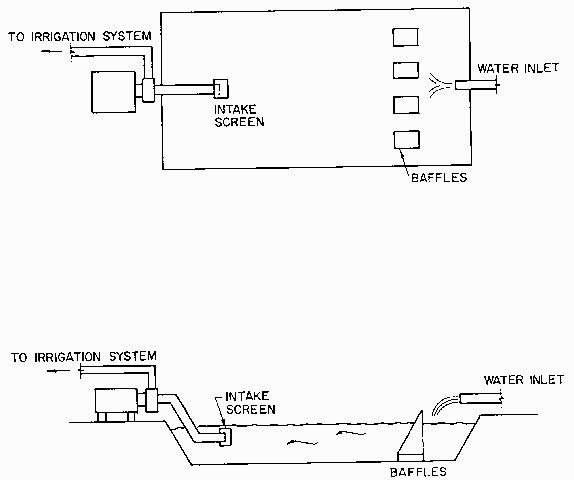
The most important consideration for the outlet is its position. Water should be removed high enough above the bottom to be free of sediments. At the same time, the outlet should be below the water surface to avoid floating contaminants (Figure 3). If the water level in the basin can fluctuate, the best solution is a floating type of entrance. In a basin where an irrigation pump is used at the outlet, the pumping levels should be controlled by floats. In the case of continuous operation, the rate of pumping must not exceed the rate of production of clean water. The turbulence effects of the inlet and outlet are included in the safety factor F.
Maintenance
A settling basin will require periodic sediment removal. The frequency of cleaning will depend on the amount of suspended solids in the water and on the F factor which was assumed in basin design. A large F value allows for more sediment and less frequent cleaning of the basin.
Example—Design of a Typical Settling Basin
An irrigation ditch with a high load of suspended mineral particles (SG = 2.67) will be used in this example of a design of a typical settling basin for a trickle irrigation system. The system requires 900 gpm, and all soil particles larger than 75 microns (200 mesh) should be removed in the basin during sedimentation. The basin will have trapezoidal cross sections and a depth of 24 inches (2 feet). The safety factor (storage factor F) is assumed to be 2.0.
First, organize all necessary design parameters:
-
The flow rate into the settling basin (Q) is 900 gpm. This is also the rate at which clean water will be produced.
-
The design settling velocity for the smallest particle to be removed (75 microns) is 12.7 inches per minute (from Figure 1). Remember that this is the settling velocity for the equivalent diameter, and it is likely that not all particles larger than 75 microns will be removed.
-
A storage factor (safety factor) F of 2.0 is assumed. This safety factor should be adequate to allow particles which are larger than 75 microns but have equivalent diameter smaller than 75 microns to settle.
-
The depth of the basin will be 24 inches, or 2 feet.
Second, use Equation 5 to calculate the mean surface area of the settling basin as shown in Equation 6.

Third, using the mean surface area in square feet (A = 227 ft2) and assuming that the length of the basin is five times its width, calculate the mean length (L) and mean width (W) from Equation 3 as shown in Equation 7.

Finally, using Equation 4, the calculated detention time is approximately 1.9 minutes for a settling velocity of 12.7 inches per minute and the selected depth of 2 feet. This is the time required to allow proper sedimentation of the particles in this basin. Actual detention time in this basin is almost 4 minutes, due to the safety factor used in Equation 5.
The design drawing of the basin is presented in Figure 2. This is the minimum basin size with a safety factor of F = 2. A larger basin will have an improved efficiency - or a larger safety factor.
References
ASAE Engineering Practice: ASAE EP405 - Design, Installation, and Performance of Trickle Irrigation Systems. 1984. Amer. Soc. Agric. Eng., St. Joseph, MI.
Boswell, M.J. Hardie Irrigation Design Manual. 1984. James Hardie Irrigation. Laguna Nigel, CA.
Jensen, M.E. Design and Operation of Farm Irrigation Systems. 1980. Amer. Soc. Agric. Eng., St. Joseph, MI.
Fair, G.M., J.C. Geyer, D. A. Okun. Water and Wastewater Engineering. 1968. John Wiley and Sons, Inc.
Salvado, J.A. Environmental Engineering and Sanitation. 1972. John Wiley and Sons, Inc.


