Introduction
There are five publications in the Savvy Survey Series that provide an introduction to important aspects of developing items for a questionnaire. This publication provides an overview of constructing indices for a questionnaire. Specifically, we will discuss why composite measures like index numbers are important, what the index number means, the difference between indices and scales, steps for the construction of indices, and recommendations for use by Extension educators. Agents should understand indices because they often deal with the evaluation of complex constructs as part of their educational programming.
Importance of Composite Measures
Extension educators are the grassroots-level workforce for cooperative Extension, and they serve their target audiences by delivering a variety of educational programs. It is a good programming practice to use data to identify client needs; and once the programs are delivered, the next responsibility of Extension professionals is to evaluate their efforts by assessing whether their target audiences made any change in their knowledge, attitudes, skills, or aspirations (KASA), as well as in their behaviors. Measuring concepts like KASA and behavior change can be a complex task, and developing questionnaire items to accurately measure these concepts is challenging. It is unlikely that you can reliably measure these complex constructs with just one questionnaire item. Instead, reliable measurement requires multiple items that are combined into an index or scale. Of course, there are many variables that can be accurately measured using just a single questionnaire item, such as age, sex, or educational attainment (Babbie 2008).
Once an Extension professional develops multiple questionnaire items for measuring a complex construct (e.g., water conservation behavior) the next challenge would be to determine how to combine these items to represent a single construct. Quantitative data analysts have developed specific techniques for calculating an index or scale for a composite measure constructed from multiple questionnaire items. Indices and scales are used frequently because they are efficient measures for data analysis and very efficient for combining multiple questionnaire items to describe a single construct (Babbie 2008). These composite measures are also likely to be more reliable and valid, which is important for accurately measuring audience needs or evaluating program outcomes. Reliability means that a question or construct provides the same answers over a period of time. It also means that similar questions for the same construct elicit responses that are consistent with each other (assuming that no educational program occurred during the interval). So, if you ask respondents how much fruit they eat every week and your respondents provide the same answer each time, then your question is reliable (Radhakrishna 2007). In addition, validity means that a question or construct is measuring what it is intended to measure. For example, if you want to measure the knowledge of healthy food choices and your questions ask for information about exercise, then your questions would not be valid measures of healthy food knowledge (Radhakrishna 2007).
Indices for a Questionnaire Construct
An index for a questionnaire construct can be defined as "a type of composite measure that summarizes and rank-orders several observations and represents some more general dimension" (Babbie 2008, 171). In other words, creating an index means accumulating the scores assigned to individual items that comprise a complex construct. Common practice for index creation is to add multiple scores into a single summary score, but there are other methods that can be used for index creation, such as the selection of items based on their importance and factor analysis.
Index Construction Logic
We will use the following example to illustrate the logic behind constructing an index. In this example, an Extension professional is interested in evaluating a program on water conservation practices. Specifically, she is interested in assessing the attitudes of program participants toward water conservation after program completion. In order to assess change in water conservation attitudes—a complex construct—she has developed several questionnaire items representing the attitude. For example, she used four statements:
- I feel good about irrigating with less during the winter season to save water.
- Turning off lawn irrigation during rainy days is convenient for me.
- It is important to me to avoid over-watering my lawn.
- I support using recycled water for lawn.
Participants were instructed to check a box for each statement to which they agreed.
In order to construct an index for attitudes toward water conservation, the Extension professional might give program participants one point for each of the four statements with which they agreed. The combined score for all statements to which a program participant agreed would then represent the attitude of that participant toward water conservation. Thus the index scores would range from 0 (the respondent agreed with none of the statements) to 4 (the respondent agreed with all of the statements).
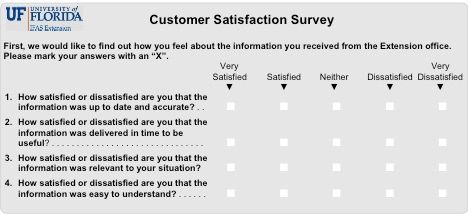
The assessment of an Extension audience's satisfaction with services offered by UF/IFAS Extension offices across the state of Florida provides another example of index construction. In order to capture information about the complex construct—satisfaction with services—an evaluation specialist developed four questions to represent the satisfaction construct (Figure 1). Each item is measured using a five-point Likert scale (1 = strongly dissatisfied, 2 = dissatisfied, 3 = neither, 4 = satisfied, 5 = strongly satisfied). To construct an index for satisfaction with Extension services, the evaluation specialist assigned a score of 1 to 5 based on the response to each statement. The index score for the satisfaction construct can range from a minimum of 4 (very dissatisfied for all four statements) to a maximum of 20 (very satisfied for all four statements). The combined satisfaction score for all four statements by each Extension client would then be used to represent the clients' overall satisfaction with Extension services.
Distinction between Indices and Scales
Many social scientists use the terms index and scale interchangeably, even though both have a specific meaning. Scales are defined as "a type of composite measure composed of several items that have a logical or empirical structure among them" (Babbie 2008, 171). Indices and scales have some things in common: both are comprised of a set of items that can be measured at the binary, ordinal, interval, or a combination of levels. For example, the items for measuring water conservation attitudes described above are binary measures that indicate whether program participants' agreed with that aspect of water conservation.
Indices and scales also have differences. On the one hand, an index is constructed by adding the scores assigned to multiple items where each item is treated equally. On the other hand, scale scores are assigned to an individual item based on the relative importance of a particular item to the complex construct (Babbie 2008). For example, some items for measuring water conservation attitudes might have a weight of two (e.g., turning off irrigation during rainy days is a good practice) while others have a weight of one (e.g., using a rain barrel is a good practice). In this example, the first statement might be weighted twice compared to the second statement because turning off irrigation during rainy days can save a lot more water than using a rain barrel.
Steps for Construction of Indices
There are four steps for constructing an index: 1) selecting the possible items that represent the variable of interest, 2) examining the empirical relationship between the selected items, 3) providing scores to individual items that are then combined to represent the index, and 4) validating the index. In the sections below, we will discuss each step in detail.
Although some Extension professionals may be unfamiliar with these steps or lack the technical skills for doing them, evaluation specialists and statisticians can be recruited to help. As Israel, Diehl, and Galindo-Gonzalez (2009) observed, Extension professionals should match the rigor of the program evaluation (including the measures used) with the importance and intensity of the program. Thus, if you are dealing with an Extension office's most important program or with a program delivered across the state, then you should examine the empirical relationship between items of an index and validate the index.
Selection of Possible Items
To illustrate the selection of items for an index in order to measure a complex construct, we will use a set of items about the knowledge of healthy food (Table 1).
When writing a set of items, carefully consider the following (Babbie 2008):
- The face validity of the items should be considered. For example, all the items about the knowledge of healthy foods in Table 1 appear to measure knowledge of healthy foods or lack thereof.
- The specificity of items should be examined and improved, if appropriate. For example, the items in Table 1 are general measures of healthy foods knowledge. Items can also be written to measure specific knowledge, such as knowledge about specific nutrients, like folic acid or vitamin D.
- The unidimensionality of items should be assessed. Unidimensionality means that all items represent a single component or facet of a concept. For example, a question about exercise should not be included in an index measuring healthy foods knowledge, even though food and exercises are empirically related to improved health.
- Consider the amount of variance among the set of items. By variance we mean that all ten items about the knowledge of healthy foods should not provide similar responses from all of the participants who are taking this test. In other words, if the answers to one item are always the same as the answers to a second item, then no new information is provided by the second item. Thus, each item should contribute some new information in measuring the construct.
Examination of the Empirical Relationship between Items
Once the items are identified, the next step is to examine the empirical relationships between items. To do so, correlation coefficients are calculated between pairs of items (using a statistical analysis software, such as SPSS). With the help of correlation analysis, we discover which items are associated with each other, and based on that association, which items need to be kept in an index (Babbie 2008). For example, if one calculates the correlations among all ten items mentioned in Table 1 and finds that the correlation coefficients among all items are 0.70 or higher, then it would be good evidence that all of the items are highly related and should be retained in an index. (Note: many reliable and valid indices have inter-item correlations that are moderate to low.) If, however, one finds that an item has low correlations with the others in the set, then this item may be a candidate for removal from the index because the item is measuring a different construct better than the one that you are trying to measure.
Scoring of Items
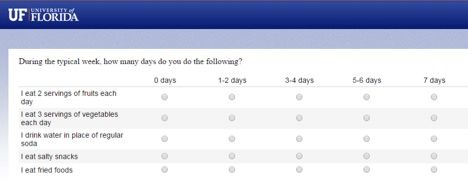
After the items for the index are finalized, the next step is to assign scores to items selected in the scale. For scoring an index, a desirable range of index scores needs to be selected. Normally, every item in an index is weighted the same. For example, the items in Table 1 were scored either 1 or 0. Items can be weighted differently if the items represent different degrees of association with the construct being measured (for example, in the case of water conservation, the statement "turning off irrigation during rainy days is a good practice" might be weighted more compared to "using a rain barrel is a good practice" because turning off irrigation during rainy days can save a lot more water than a rain barrel) (Babbie 2008). In Figure 2, all healthy food behavior items are weighted equally, and each score ranges from one to five. Consequently, the overall index ranges from a minimum of 5 to a maximum of 25. The primary advantage of using an index for a construct is that we have more gradation in the measurement of a particular construct when compared to the individual items (Babbie 2008). This helps Extension professionals to better measure complex constructs like knowledge of healthy food. When creating an index from the scores of a set of items, missing data can be a problem. Please refer to Appendix A for detailed information about strategies for addressing missing data.
Validation of Index
In the previous three steps, we discussed the selection and scoring of items that produce a composite index to measure a complex variable. To justify the composite measure resulting from the previous three steps, we need to validate our index, or test the index for validity and reliability. For example, the items in Table 1 will represent a good index of healthy food knowledge if the index is able to rank-order students based on their knowledge of healthy foods (Babbie 2008).
An index can be validated using internal validation. In internal validation, which is also called item analysis, the composite measure is examined for how well it relates to individual items in the index. Item analysis also means that an individual item makes an independent contribution to the composite index; otherwise, a particular item would just be duplicating the effect of the other items included in the composite index (Babbie 2008).
Internal validation of an index can be done in a variety of ways, but two common methods include calculating Cronbach's alpha and conducting factor analysis. Cronbach's alpha measures the internal consistency of the items. Cronbach's alpha is a procedure available in all major data analysis software (like SPSS, SAS, STATA, R), and it can help to validate the index by determining the average correlation among various items included in the index (Santos 1999). Although a Cronbach's alpha of 0.70 or higher is considered an acceptable measure of the internal consistency of index statements (Santos 1999), other Extension professionals believe 0.80 is a more appropriate threshold (Willits, F., personal communication, May 17, 1979; Peterson 1994). Factor analysis is an advanced method for establishing the internal validity of an index. Please refer to Appendix B for detailed information on factor analysis.
Conclusions and Recommendations for Extension Educators
It is the Extension professionals' responsibility to report the change in KASA and behaviors of their target audiences resulting from educational programs they deliver. KASA and behavior change are often complex constructs and it is very hard to measure them using a single statement. Using a composite measure, such as an index, can be a valuable tool for measuring the impact of programs. An index can be a more valid and reliable way to measure a particular construct. We advise Extension professionals to use indices and scales for assessing needs and evaluating program outcomes. Interested readers may wish to read the complete Savvy Survey Series to get more detailed information about how to develop better surveys.
References
Babbie, E. 2008. The basics of social research. Belmont, CA: Thomson Wadsworth.
Fetsch, R. J., and R. K.Yang. 2005. "Cooperative and competitive orientations in 4-H and non-4-H children: A pilot study." Journal of Research in Childhood Education, 19(4), 302–313. https://doi.org/10.1080/02568540509595073
Israel, G.D., D. Diehl, and S. Galindo-Gonzalez. Evaluation situations, stakeholders & strategies.WC090. Gainesville: University of Florida Institute of Food and Agricultural Sciences, 2009. https://edis.ifas.ufl.edu/publication/WC090
Mertler, C. A., and R.A.Vannatta. 2002. Advanced and multivariate statistical methods. Los Angeles, CA: Pyrczak Publications.
Peterson, R. A. 1994. "A meta-analysis of Cronbach's coefficient alpha." Journal of Consumer Research, 21(2), 381-391. https://doi.org/10.1086/209405
Radhakrishna, R. B. 2007. "Tips for developing and testing questionnaires/instruments." Journal of Extension, 45(1), 1TOT2. https://archives.joe.org/joe/2007february/tt2.php
Santos, J. R. A. 1999. "Cronbach's alpha: A tool for assessing the reliability of scales." Journal of Extension, 37(2), 2T0T3. https://archives.joe.org/joe/1999april/tt3.php
Schafer, J. L., and J.W. Graham. 2002. "Missing data: Our view of the state of the state of the art." Psychological Methods, 7(2), 147–177. https://doi.org/10.1037/1082-989X.7.2.147
Appendix A: Missing Data Problems in an Index
One limitation of indices and scales is the problem of missing data. It is difficult to get a 100% response rate for each item or question and most surveys are missing some data. In order to construct and use the index properly, we must understand how to handle the missing data. If just a few participants have missing data, then we can choose to exclude those cases from the analysis (Babbie 2008). If we have a higher number of participants with missing data, then excluding these cases from the data analysis is not a feasible option. Instead, missing data can be handled in a number of ways, such as replacing the missing data with the midpoint of the response scale, such as 3–4 days (3) in Table 2, or replacing the missing data with the mean score for the item (Babbie 2008). Currently, statisticians recommend using single or multiple imputations to address missing data (e.g., Schafer & Graham 2002). Most current data analysis software (e.g., SPSS, SAS, STATA, R) include imputation procedures. On the one hand, excluding participants with missing data can cause bias and, on the other hand, assigning values to missing data can influence the nature of findings and the interpretation of index scores. A decision must be made, based on the objectives of your study, about how to handle the missing data (Babbie 2008).
Appendix B: Factor Analysis for Index Construction
Factor analysis is a more robust method of validating an index. Factor analysis is a process in which different items (or variables) that represent a similar concept are clustered together. Factor analysis can also be defined as a process by which we determine how the different statements in an index overlap with each other; that is, it measures the amount of shared variance among a set of items/variables in an index (Mertler and Vannatta 2002). The main output in factor analysis are factor loadings, which define the correlation of an individual statement/variable with a complex construct (also called a component or factor). The factor loadings values range from -1 (perfect negative correlation with the factor) to +1 (perfect positive correlation with the factor). Variables/ items in a composite index can have loading on multiple factors but each should have high loading on only one factor (Mertler and Vannatta 2002).
Table 2 provides an example of factor analysis from a study of 4-H children where Fetsch and Yang (2009) constructed a questionnaire to measure the competitive and cooperative orientations of 4-H and non-4-H children. In order to assess which statements in the questionnaire represent which concept, they conducted the factor analysis. In Table 2, the seven statements were found to load to three factors: unconditional parental support (three statements), cooperative orientation (two statements), and competitive orientation (two statements) with a factor loading of 0.73 or higher. The three factors indicate that the seven items measured three distinct dimensions rather than a single dimension. In some situations, it is desirable to have an index for each of the dimensions, while in other situations the goal may be to have a set of items that form a unidimensional index with one factor.