Southern pine forests provide timber value and many environmental amenities such as carbon sequestration, water quality and quantity, air quality, recreation biodiversity, and wildlife habitats. Given the important role that these forests play in the country's economy and society, economic valuation of forest resources helps us to make important decisions about the sustainable management of forest lands. This publication will provide a guide for forest landowners, managers, and stakeholders in conducting a valuation of timber investments. We will review and provide examples of two different approaches for determining the optimal rotation age of even-aged forest stands: the biological rotation, the single rotation and the land expectation value.
The Biological Rotation
A landowner could choose to clearcut the forest stand at the age at which the production of timber volume is maximized. To illustrate this method, it is necessary to first define two forestry concepts: the mean annual increment (MAI or average growth of the forest) and periodic annual increment (PAI or changes in timber volume between two periods). We can define MAI and PAI as follows:
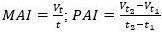
where Vt is the stand volume at age of the stand t, and Vt2 and Vt1 are the stand volumes at ages of the stand t2 and t1, respectively1. Early in an even-aged stand's growth, PAI is positive (each year more timber volume than the previous year); MAI is also positive, but it is growing at a slower rate compared to PAI. As the stand matures, PAI begins to "flatten," and then begins to drop (less timber volume growth next year) as growth rates slow, until PAI is the same as the long-term average annual growth in timber volume (MAI) – MAI = PAI. At this point, MAI is maximized, and it is time to clearcut for a landowner using the biological rotation to determine the optimum time to clearcut.
Table 1 illustrates the biological rotation approach considering slash pine as an example. For example, at stand age 20 years, the volume of the stand V10 = 158.0 tons/ acre. At age stand 21 years, the volume of the stand V21 = 167.3 tons/acre. Thus, at stand age 21 years, the MAI = 8.0 tons/acre/year (167.3/21), while the PAI = 9.3 tons/acre/year ((167.3 - 158.0)/(21 - 20)). Using this valuation method as a guide, the landowner or manager should harvest the stand when the MAI curve intersects the PAI curve from below, which occurs at stand age 24 years (Figure 1).
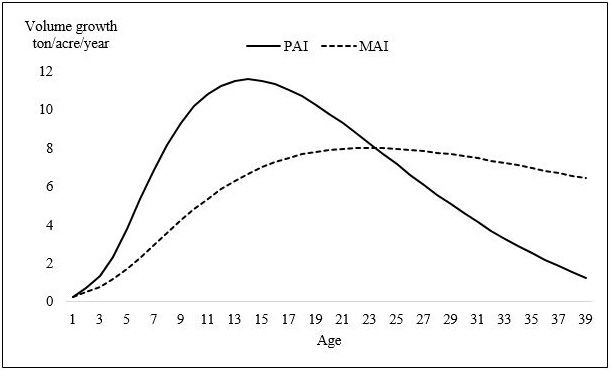
The drawback of this approach is that, while high timber growth rates are clearly economically beneficial, landowners maximize the volume of timber but not the value of the timber. For instance, let us consider a stand that has reached its maximum MAI but where an additional year of growth might allow a significant portion of the trees to grow from pulpwood to chip-n-saw (and the landowner to recoup the resulting 50% or more change in value).
The Single Rotation and Land Expectation Value
The single rotation determines the present value of the total timber benefits minus the present value of the of the total silvicultural costs over a one-rotation cycle—the net present value (NPV). Here, the timber benefits are realized in the future when the forest stand is thinned or finally clearcut. Likewise, some silvicultural costs and management costs can be incurred in the future as the forest stand is growing. This implies that the total timber benefits and silvicultural and management costs have to be discounted back to present. This method uses the time value of the money, i.e., the value of money in the present compared to the same amount of money received in the future on an annual compound basis. The rationale behind this is that the money can be reinvested and earn interest. For a single rotation, the NPV of a forest stand for timber production is:
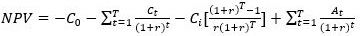
where C0 is the establishment costs (site preparation and planting costs at stand age 0); Ct is the intermediate costs to grow the stand at time t (e.g., fertilization, marking, thinning costs); Ci is the annual management or administrative costs; At is the economic revenues due to thinning benefits and final harvest of the stand; and is the discount rate.
The single rotation model does not consider that the landowner, once the forest stand is harvested, can replant it again. However, the landowner, and future owners, can decide to grow a forest stand on the land in perpetuity. The land expectation value approach is the present value of perpetual cash flows of costs and timber revenues starting from bare land (Faustmann 1849). This model assumes a perpetual cycle of clearcut and replant. It represents the value of the bare land for growing timber, forever. Thus, the land expectation value approach (LEV) of a forest stand for timber production can be defined as:
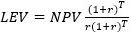
Let's consider the following forest investment in a slash pine stand (Table 2). It is assumed that the slash pine stand is planted at time t = 0 and harvested at age T = 25 years. The stand produces three forest products, sawtimber, chip-and-saw, and pulpwood, using the same growth and yield model used for the biological rotation method. Silvicultural activities, with their associated current costs and revenues (cash flows), occur at the times specified in Table 2. A discount rate r = 0.03 (3%) is also assumed.
Thus, the net present value of single rotation and the land expectation value for timber production is:
= 40070/1.03570/1.031270/1.0316300/1.0312300/1.031620(1.0351)/0.03(1.0325)
90/1.0312 340/1.0316 1,900/1.0325 = $875 per acre.
= (875)(1.03)25/0.03(1.03)25 = $1,675 per acre.
In this example, the time to clearcut the forest stand is fixed at 25 years. However, a rotation age should be calculated for a timber investment as part of the optimal forest management. This requires us to determine the clearcut time that maximizes the net present value and land expectation value of the forest investment. In the example above, this occurs at age 27 and 30 years with a LEV = $1,739 per acre and NPV = $991 per acre, respectively (Figure 2). Under the LEV approach, rotation age is shorter than the rotation age of the one rotation single model. Depending on the type of forest species and silvicultural treatments (slow or fast-growing stand), the rotation age obtained with the biological rotation can be longer or shorter than the optimal rotation age obtained with the LEV approach (Binkley 1987).

The Land Expectation Value and Nontimber Benefits
The LEV formula can also be adjusted to include nontimber benefits such as hunting leases, carbon sequestration, and biodiversity values (Hartman 1979). Thus, using Equation 3 and denoting as the amenity values over time , the land expectation value of timber and nontimber benefits LEVb is now as follows:
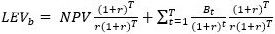
Let's assume now that the landowner also considers hunting leases ( with a value of $10 per acre per year, and that hunting leases start when the age of the stand is 10 years old. At age 25 years, the sum of the present value of hunting leases is $96 per acre. Thus, the LEVb of a fixed 25-year-old forestry investment is 1,675 + (96)1.0325/(0.03[1.03]25) = $1,859 per acre
Plugging our numbers from the original example into this formula, the optimal rotation age with another enterprise factored in is 28 years with a LEVb = $1,932 per acre (Figure 2). In this case, the optimal rotation age is longer than the rotation age obtained in the case of the timber production. The reason is that, although we have assumed a constant value for nontimber benefits, the value of this amenity is initially considered when the stand is 10 years old. If the value of the amenity is constant over the age of the stand, i.e., starting at year 1, the optimal rotation age is the same as in the case of the timber production. In general, if the nontimber benefit changes with the age of the stand, then the optimal rotation age changes compared to the optimal rotation age associated with timber production.
Conclusions
The biological rotation approach determines the optimal time at which a forest stand can be harvested to maximize timber production. However, this approach ignores costs and revenues that can be obtained from the forest. The net present value (NPV) determines the value of a forest stand considering a single rotation. The land expectation value (LEV) estimates the value of a forest stand considering timber benefits, costs, and interest rate and assuming forestry use in perpetuity. It also determines the optimal rotation age in which a stand should be harvested and regenerated. The LEV rotation age can be shorter or longer compared to the rotation age of the biological rotation method. The LEV rotation age is always shorter compared to the rotation age of the single rotation method. The LEV method can be also adjusted to incorporate nontimber benefits. These methods can help forest landowners and managers in making forest investment decisions.
Notes
1 A variation of PAI is the current annual increment (CAI). In this case, the growth in timber volume occurs in the current year.
Literature Cited
Binkley, C. 1987. "When is the optimal economic rotation longer than the rotation of maximum sustained yield?" Journal of Environmental Economics and Management 14(2): 152–158.
Faustmann, M. 1849. "Calculation of the value which forest land and immature stands Possess." Reprinted in Journal of Forest Economics (1995) 1(1): 89–114.
Hartman, R. 1976. "The harvesting decision when a standing forest has value." EconomicInquiry 14(1): 52–55.
Pienaar, L. V., B. D. Shiver, and J. W. Rheney. 1996. Yield Prediction for Mechanically Site-Prepared Slash Pine Plantations in the Southeastern Coastal Plain. PMRC Technical Report 1996-3A, University of Georgia, Athens, GA.
Maggard, A., and R. Barlow. 2017. "2016 Costs and trends for southern forestry practices." Forest Landowner Magazine September/October, 31–39.
Timber Mart South, 2018. US South Annual Review: 2018. University of Georgia Warnell School of Forestry and Natural Resources, Center for Forest Business, and Frank W. Norris Foundation, Athens, GA.