A microirrigation system has the potential to be a very efficient way to irrigate. However, to be efficiently applied, irrigation water must be uniformly applied. That is, with each irrigation, approximately the same amount of water must be applied to all of the plants irrigated. If irrigation is not uniformly applied, some areas will get too much water and others will get too little. As a result, plant growth will also be nonuniform, and water will be wasted where too much is applied. Uniformity is especially important when the irrigation system is used to apply chemicals along with the irrigation water because the chemicals will only be applied as uniformly as the irrigation water.
The uniformity of water application from a microirrigation system is affected both by the water pressure distribution in the pipe network and by the hydraulic properties of the emitters used. The emitter hydraulic properties include the effects of emitter design, water quality, water temperature, and other factors on emitter flow rate. Factors such as emitter plugging and wear of emitter components will affect water distribution as emitters age.
This publication presents procedures to separately evaluate the effects of pressure variations in the pipe network (hydraulic uniformity) and variations due to the emitter characteristics (emitter performance variation) on uniformity of water application. Knowing both of these factors will help an irrigation system manager identify the causes of low application uniformities and the corrections that may be required to improve the uniformity of water application.
These procedures should be used on newly installed microirrigation systems to verify that they were properly designed and installed, and to provide a reference for future evaluations. Also, evaluations should be done each year to determine the effects of emitter plugging or changes in other components on system performance. More frequent evaluations may be required to diagnose and treat emitter plugging problems.
Flow Rate Variation and Uniformity
The uniformity of water application can be calculated from the statistical distribution of emitter flow rates that are measured in the field.
where U S = statistical uniformity of the emitter discharge rates, and V qs = statistical coefficient of variation of emitter discharge rates.
In Equation (1) , the coefficient of variation is the standard statistical definition of the sample standard deviation divided by the mean. Thus, when emitter flow rates are measured in the field, V qs includes the effects of variability in emitter flow rate from all causes, including both water pressure distributions and emitter hydraulic properties, emitter plugging.
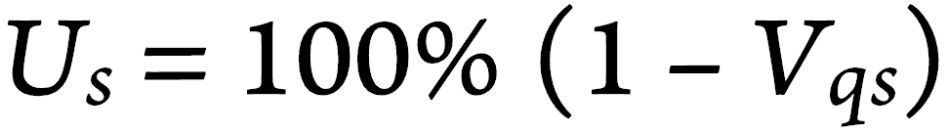
From Equation (1), when the variation in emitter flow rates increases, the uniformity of water application decreases. Table 1 lists five microirrigation uniformity classifications, ranging from excellent to unacceptable, recognized by the American Society of Agricultural Engineers (ASAE, 1996a; 1996b).
Emitter Hydraulic Characteristics
Emitter Flow Equation
Microirrigation emitter flow rates have different responses to pressure variations. The response of a specific emitter depends on its design and construction. The relationship between emitter operating pressure and flow rate is given by:
where
q= emitter flow rate (gal/hr),
K d = emitter discharge coefficient,
P= operating pressure (psi), and
x= emitter discharge exponent.
The coefficient and exponent for this equation will normally be given by the emitter manufacturer or from an independent testing laboratory such as the California State University Center for Irrigation Technology (CIT).
The emitter discharge exponent, x, is a measure of the sensitivity of the emitter flow rate to changes in pressure. This exponent is dimensionless and it is independent of the units used to measure flow rate and pressure. Values of x range from 0 to 1, with values around 0.5 being very common for turbulent flow emitters. Low values of x (below 0.5) indicate emitters that are relatively insensitive to changes in pressure (pressure compensating emitters), while large values of x indicate emitters that have larger changes in flow rate as pressures change (laminar flow emitters).
Emitter Manufacturing Variation
In addition to flow variations due to pressure, variations between emitters of the same type also occur due to manufacturing variations in the tiny plastic components. Because their orifice diameters are very small, microirrigation emitters are easily plugged or partially plugged from particulate matter, chemical precipitates, and organic growths. For these reasons, water application uniformity may be greatly affected by the emitter performance.
The manufacturing coefficient of variation (V m) is defined as the statistical coefficient of variation (standard deviation divided by the mean discharge rate) in emitter discharge rates when new emitters of the same type are operated at identical pressures and water temperatures. Under these identical operating conditions, differences in flow rates observed are assumed to be due to variations in emitter components. Table 2 classifies point source (drip emitters and microsprinkiers) and line source (drip tubing) emitters based on manufacturing variation.
Because manufacturing variation reduces uniformity of water application, choose emitters with low values of V m. When comparing emitters with similar flow properties (i.e., similar values of K d and x in Equation 1), the highest uniformity will be obtained by selecting the emitter with the smallest manufacturing variation.
Pressure Variation and Uniformity
When water flows through a pipe network, pressure losses occur because of friction losses in the pipes and fittings. Pressure changes also occur as water flows uphill (pressure loss) or downhill (pressure gain) in a pipe network. If a microirrigation system is poorly designed or improperly installed, pressure losses may be excessive because components are too small for design flow rates or slopes are too steep for the components selected. For these reasons, water application uniformity may be greatly affected by the design of the pipe network.
Hydraulic uniformity refers to the effects of pressure variations on the uniformity of water application from a microirrigation system. Hydraulic uniformity, U sh , is defined similar to water application uniformity in Equation (1), except that the emitter discharge exponent, x, must also be considered. This exponent shows the relationship between emitter operating pressure and flow rate. Because x is different for different types of emitters, the allowable pressure variation is also different for each emitter type.
where
U sh = hydraulic uniformity based on pressure distributions,
x= emitter discharge exponent, and
Vh= hydraulic variation, which is the statistical coefficient of variation of pressures.
A low value of U sh is most often due to improper design. However, improper installation of components or the installation of the wrong components can also reduce U sh. Low values of U sh may be due to pipe sizes that are too small, laterals that are too long, laterals that are incorrectly oriented with respect to slope, improper emitter selection, or other causes. All of these items must be properly designed and installed in order to obtain an acceptable uniformity of water application.
Uniformity Tests
This publication presents procedures for making three separate tests that are useful to evaluate the performance of a microirrigation system: (1) overall water application uniformity, (2) hydraulic uniformity or pressure variation, and (3) emitter performance variation. These tests should be performed in the order indicated because, if the overall water application uniformity is high, there is no need to perform further tests. If the water application uniformity is low, then hydraulic uniformity tests should be conducted in order to determine the cause of the low uniformity. The hydraulic uniformity test will indicate whether the cause of the low water application uniformity is excessive pressure variation in the system or emitter performance problems such as plugging.
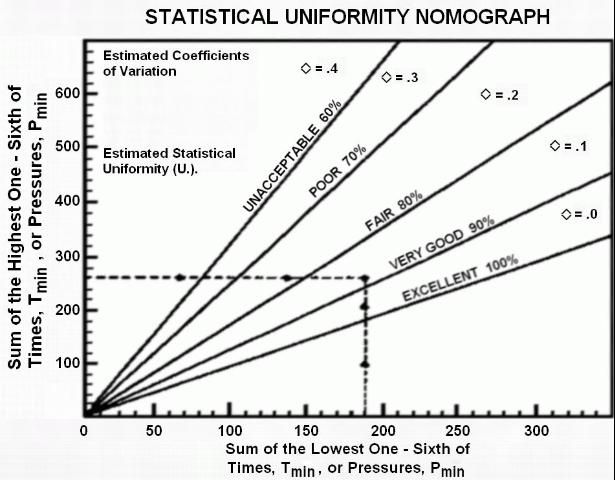
To simplify computations, the statistical uniformity nomograph shown in Figure 1 was developed. This graph is used to determine both water application uniformity from emitter flow rate data and hydraulic variation from pressure distribution data.
1. Water Application Uniformity Test
The water application uniformity is a measure of how evenly the volumes of water are applied from each emitter. This uniformity can be determined by measuring emitter flow rates or the times required to fill a container of known volume. If some emitters tested are completely plugged, then flow rates must be measured since a container will never be filled. To measure emitter flow rates, use a graduated cylinder to measure the volume collected for a given time, such as one or two minutes. A stop watch or wrist watch with a second hand can be used to measure times.
To accurately determine uniformity, measurements should be made at a minimum of 18 points located throughout each irrigated zone. More may be required for greater accuracy. Computations will be simplified if the number of points measured is a multiple of 6. The statistical coefficient of variation is then calculated from these data points.
Care should be taken to distribute the measurement points throughout the irrigated zone. Some points should be located near the inlet, some near the center, and some at the distant end. Also, some should be located at points of high elevation and some at points of low elevation. However, the specific emitters to be tested should be randomly selected at each location. Do not visually inspect the emitters to select those with certain flow characteristics before making measurements. In fact, to avoid being influenced by the appearance of an emitter as it operates, emitters could be selected and flagged before the irrigation system is turned on. The water application uniformity can be read from Figure 1. The following 6 steps are required:
- Calculate 1/6 of the number of data points measured. That is, divide the number of data points by 6. For example, if 18 points were measured, this number will be 3.
- Look at the set of data measured to locate and then add the lowest 1/6 of the flow rates (or times or volumes) measured. For 18 data points this will be the sum of the 3 lowest flow rates, times or volumes measured.
- Look at the data set again to locate and then add the highest 1/6 of the flow rates, times, or volumes measured. For 18 data points this will be the sum of the 3 highest values.
- Locate the sum of the high flow rates, times, or volumes on the vertical axis in Figure 1. Draw a horizontal line across the graph from that point. If this sum does not fit on the scale, or if the value is very small so that the scale is difficult to read, the sums calculated in Steps 2 and 3 can both be multiplied or divided by a common factor. This can be done because their absolute values are not important, but only the relative differences between the high and low values are critical.
- Locate the sum of the low flow rates, times or volumes on the horizontal axis in Figure 1. Draw a vertical line up the graph from that point. Again, if necessary, modify the values from Steps 2 and 3 as discussed in Step 4. However, if changes are made, be sure to change the sums of both the lowest and highest values by multiplying or dividing both by the same factor.
- Read the water application uniformity at the intersection of the two lines drawn.
As an example of the use of Figure 1, assume that water from 18 emitters was collected at random locations throughout an irrigated zone. Assume that the method used was to record the times required to fill a small container, and that the times were recorded in seconds. An example set of data is shown in Table 3.
From the above 6-step procedure:
Step 1. 1/6 of l8 data points = 3
Step 2. 62 + 64 + 64 = l90 sec (lowest 3 values)
Step 3. 90 + 88 + 86 = 264 sec (highest 3 values)
Step 4. locate 264 sec on the vertical axis in Figure l and draw a horizontal line across the graph from that point.
Step 5. Locate 190 sec on the horizontal axis in Figure 1 and draw a vertical line from that point.
Step 6. The intersection of these two lines occurs between the 80% and 90% lines. This indicates a "Very Good" water application uniformity coefficient of about 88%.
From this analysis, it can be concluded that the irrigation system represented by the flow rate data in Table 3 was designed and constructed to achieve a high degree of uniformity of water application throughout the zone that was analyzed. Also, because of the high water application uniformity, it can be concluded that the variability among emitters used in this irrigation system is low. No significant emitter plugging is indicated.
2. Hydraulic Uniformity (Pressure Variation) Test
The hydraulic uniformity of a microirrigation system is estimated by measuring pressures at points distributed throughout each irrigated zone. Measure pressures to the nearest pound per square inch (psi). Although it is not necessary to measure pressures at the same emitters where flows were measured, it is normally convenient to do so while flow rates are being measured.
Pressures can easily be measured using a portable pressure gauge connected with a flexible tube. Gauges are commercially available with a needle on a flexible tube for direct insertion into the lateral pipe. Alternatively, some emitters are constructed so that a flexible tube can be slipped over the emitter, allowing the pressure to be measured with the emitter in place.
Some microsprinkler emitters are connected to the lateral using small diameter flexible tubing with a barbed insertion fitting. Because of pressure losses in these connecting tubes, pressure should be measured at the end of the tube near the emitter while the emitter is operating. This can be done by installing a small barbed tee in the connecting tube.
The pressure distribution data are analyzed in the same way that the previously discussed flow rate data were analyzed. The only difference is that the hydraulic coefficient of variation due to pressure, V h, is read from Figure 1 rather than directly reading the statistical uniformity. Then, in Step 7, the hydraulic uniformity must be calculated from V h and the emitter discharge exponent, x, as shown in Equation (3). The hydraulic uniformity can be determined using the following 7-step procedure:
- Calculate 1/6 of the number of data points measured. If 18 pressures were measured, this number is 3.
- Look at the data measured to locate and then add the lowest 1/6 of the pressures measured. For 18 pressure measurements, this is the sum of the 3 lowest pressures.
- Look at the data again to locate and then add the highest 1/6 of the pressures measured. For 18 pressure measurements, this is the sum of the 3 highest pressures.
- Locate the sum of the high pressures on the vertical axis in Figure 1. Draw a horizontal line across the graph from that point. If this sum does not fit on the scale, or if the value is very small so that the scale is difficult to read, the sums in Steps 2 and 3 can both be multiplied or divided by a common factor.
- Locate the sum of the low pressures on the horizontal axis in Figure 1. Draw a vertical line up the graph from that point. Again, if necessary, modify the values from Steps 2 and 3 as discussed in Step 4. However, if modifications are made, be sure to modify the sums of both the lowest and highest values by multiplying or dividing both by the same factor.
- Read the hydraulic variation, V h, at the intersection of the two lines drawn.
- Calculate the hydraulic uniformity, U sh, from Equation (3).
As an example of the use of Figure 1 to calculate the hydraulic uniformity, consider the pressure data set in Table 3. Assume that the 18 pressures shown in Table 3 were read at random locations throughout the irrigated zone. It will normally be easiest to measure these pressures at the same time and location while the flow rates were being measured, but this is not necessary. For example, they could be measured later at 18 different locations, after the flow rate data indicated that there was a problem with water application uniformity, and it is now important to determine the cause of that low uniformity.
For this analysis, the emitter discharge exponent, x, must be obtained from the emitter manufacturer for the emitter being used. For this example assume that a typical turbulent flow emitter was used with x = 0.5. Then, following the above 7-step procedure:
Step 1. 1/6 of 18 = 3
Step 2. 21 + 21 + 22 = 64 psi (1owest 3 values)
Step 3. 28 + 27 + 27 = 82 psi (highest 3 values)
Step 4. Because the data from Steps 2 and 3 would be located in the lower left-hand corner of Figure 1, and the graph would be difficult to read, multiply both values by 5 to expand the scale:
(5)(82 psi) = 410 psi
(5)(64 psi) = 320 psi.
Then locate 410 psi on the vertical axis in Figure 1 and draw a horizontal line across the graph from that point
Step 5. Locate 320 psi on the horizontal axis in Figure 1 and draw a vertical line from that point.
Step 6. The two lines drawn intersect at Vh = 0.1, indicating a hydraulic uniformity that falls between the "Very Good" and "Excellent" categories.
Step 7. From Equation (3), calculate U sh:

U sh = 100% (1.0 - (0.5)(0.1)) = 95%
From Figure 1, this hydraulic uniformity would be classified in the "Excellent" category.
From the above analysis, it can be concluded that the irrigation system represented by the pressure data in Table 3 was designed and constructed to achieve a high degree of uniformity in pressures throughout the zone that was analyzed. Thus, if a low water application uniformity was previously indicated, the cause of that low uniformity is not poor hydraulic uniformity. Rather, the cause is emitter performance, probably emitter plugging.
3. Emitter Performance Variation Evaluation
Emitter performance variation, V pf , refers to non-uniformity in water application that is caused by the emitters. If the emitter performance variation is high, this is normally due to emitter plugging or to manufacturing variation among emitters. It may also be due to other factors which affect emitter flow rates, such as temperature.
Emitter performance variation can be evaluated by measuring emitter flow rates at known pressures. This can be done by removing the emitters and testing them in a laboratory. Alternatively, both pressures and flow rates can be measured at individual emitters, but then flow rates must be corrected to a common pressure by using the manufacturer's data for that emitter. Neither of these procedures are recommended because of the amount of labor involved for each.
The nomograph in Figure 2 simplifies the procedure for determining the emitter performance variation from the hydraulic and water application uniformities. The emitter performance variation can be estimated in the following three steps:
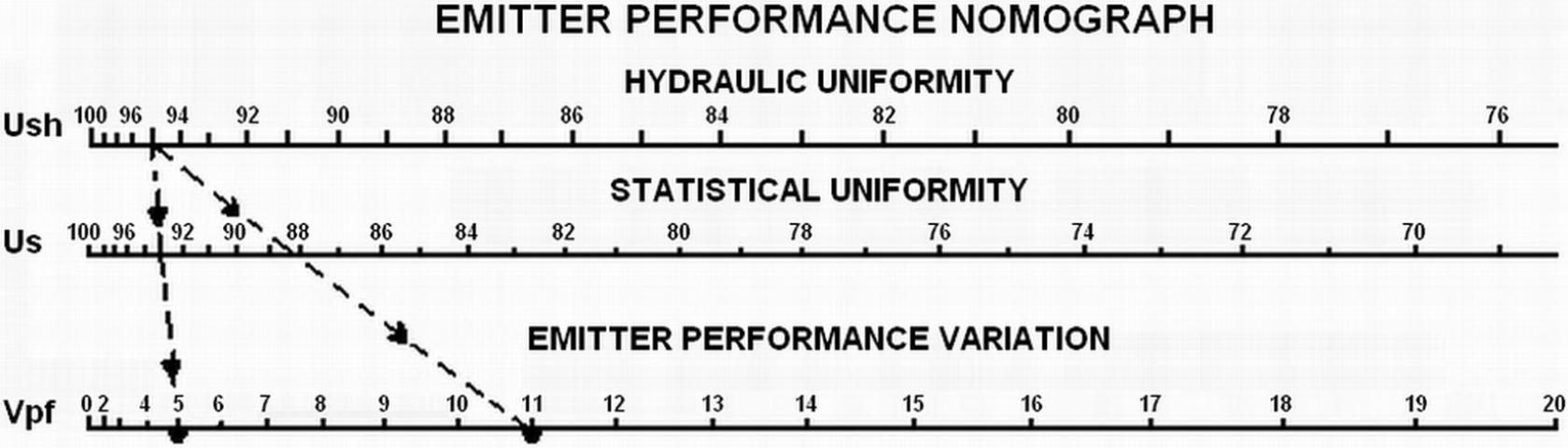
- Locate the previously calculated hydraulic (pressure) uniformity coefficient, U Sh, on the upper bar of the nomograph.
- Locate the previously calculated water application uniformity coefficient, U s, on the center bar of the nomograph.
- Draw a straight line fom the measured hydraulic uniformity (upper bar), through the water application uniformity (center bar), and extend it down to the lower bar. Read the emitter performance variation V pf on the lower bar.
As an example, assume that the uniformity of a new microirrigation system was measured immediately after installation, and that the hydraulic uniformity determined from pressure measurements was 95%. Also, assume that the statistical uniformity of water application from emitter flow rate measurements was 93%. From Figure 2, a straight line drawn through U sh = 95% and U s = 93% intersects the lower bar at an emitter performance variation of 5%. This value would be expected to be approximately the coefficient of manufacturing variation for the emitter because this system is newly installed, and it is assumed that no emitter plugging has yet occurred. For this example, both the hydraulic and water application uniformities are above 90% and would be classified as excellent, indicating that the system was well-designed and properly installed.
As a second example, assume that the same irrigation system was again evaluated after operating for 6 months, and that the hydraulic uniformity was again found to be 95%, but the water application uniformity was now 88%. From Figure 2, a straight line drawn through these two pomts shows that the emitter performance variation increased to 11%. These results demonstrate that the cause of the lower water application uniformity measured is a change in emitter performance, probably emitter plugging. This suggests that chemical water treatment or flushing of lines may be required to restore the system to its original high uniformity.
Because the U sh remained unchanged, this demonstrates that a change in the hydraulics of the system was not the cause of the lower application uniformity measured. Thus, these tests not only indicate whether a problem with water application uniformity has occurred, but also whether the changes were due to changes in the system hydraulics or changes in the emitter performance.
Accuracy of Estimates
The estimates of uniformities and performance variations made using the methods presented in this publication are based on statistical samples of pressures and flow rates measured in the field. As with any statistical estimate, the results will not be completely accurate unless all emitters are sampled. Thus, it is necessary to consider confidence limits on the estimates made when only a few emitters are sampled. This is a method of estimating how accurate the measured result is, and whether it is necessary to make additional measurements to improve the accuracy. Table 4 gives confidence limits on the uniformities or variabilities measured.
From Table 4, the confidence limits are smaller when the uniformity is greater. For example, for 18 samples, the confidence limit is ±3.5% if the uniformity measured was 90%, while the confidence limit is ±16.2% if the uniformity measured was 60%. This means that the actual uniformity would be expected to be in the range of 86.5% to 93.5% (90% ± 3.5%) if the estimated value was 90%, while it could be expected to range as much as 43.8% to 76.2% (60% ± 16.2%) if the estimated value was 60%. The smaller confidence limits occur at the higher uniformities because it is not likely that samples would be randomly selected that would indicate a high uniformity if the uniformity was actually low.
From Table 4, the confidence limits decrease as more samples are taken. This indicates that we are more confident in the results if more measurements are made. In fact, the confidence limits decrease by a factor of two when the number of samples is multiplied by four. If the uniformity estimates are low when only 18 samples are taken, then more samples must be taken in order to improve the confidence in the estimate. Thus, Table 4 can be used to determine the number of samples that must be taken in order to estimate the actual uniformity with the desired accuracy.
Summary
A method was presented to evaluate microirrigation uniformity of water application under field conditions. As a minimum, emitter flow rate data are required for these evaluations. Pressure data are also needed in order to determine whether the cause of any low uniformity observed is system hydraulic (pressure) problems or emitter characteristics, including plugging. If both tests are made, the results not only indicate whether a problem with water application uniformity exists, but also demonstrate whether the problem is due to system hydraulics or to emitter performance, so that appropriate corrective actions can be taken.
References
ASAE. 1996a. Field evaluation of microirrigation systems. EP405.1. ASAE Standards. Amer. Soc. Agric. Engr., St. Joseph, MI. Pp. 756-759.
ASAE. 1996b. Design and installation of microirrigation systems. EP409. ASAE Standards. Amer. Soc. Agric. Engr., St. Joseph, MI. Pp.792-797.