Introduction
Artificial intelligence, specifically machine learning (ML) applications, have emerged as essential modeling tools for scientists, technicians, and decision-makers who seek insights into complex processes with interrelated variables, such as natural resources management. ML has also become more popular for practical decision-making when other modeling tools are unavailable. However, determining the minimum amount, granularity, and quality of input data for these ML applications is not always straightforward. This publication is intended for scientists, technicians, and decision-makers who want to start using ML in their projects. It provides an overview of the factors that should be considered when employing ML applications with time series (TS) data as input. Although the information in this publication could be relevant to projects using images as input data, additional checks on these images would be required to address data quality. For more examples of object detection AI applications, refer to Ask IFAS publication AE529, "Applications of Artificial Intelligence for Precision Agriculture."
Influence of Domain Knowledge on ML Models
Although ML algorithms are data-driven modeling approaches, the scientific or engineering theory behind the system being studied is critical to determine the validity of ML predictions. Domain knowledge can guide the application of ML as it guides the understanding of the underlying concepts of the system of interest and the purpose of the specific project. Domain knowledge also allows for the identification of relevant features, the formulation of hypotheses, and the interpretation of results. The initial feature selection using domain knowledge has a positive impact on the ML prediction, especially when the relationships between features are uncertain. It is important to note that as more features are selected, the ML model becomes more complex and requires a larger data set.
How much data should I collect to use ML?
Because ML models are data-driven, having more observations is more beneficial. More observations facilitate the accurate capture of patterns, trends, and variations in TS data. While there is no established minimum threshold for the number of observations required to use ML, several factors should be considered, including:
- Data granularity and complexity: Collecting data frequently would increase the size of the TS data set. However, higher-frequency data collection might be costly and may not necessarily add value to ML forecasting (Rostami-Tabar et al. 2023). As more data is collected, the complexity of ML models required to process it also increases. The minimum number of data points in a TS can be related to the number of features and parameters an ML algorithm must consider. TS with multiple cycles or repetitions would be preferable to those derived from multiple sites but with only one cycle or repetition. For instance, in an irrigation management experiment where data is collected using soil moisture sensors for one month with three irrigations per week, collecting data every minute might not improve ML forecast compared to data collected every 15 to 30 minutes. However, TS with a higher number of irrigation events, such as data spanning one year, could potentially improve the forecast.
Furthermore, consider the scenario where TS data is obtained from 12 sensors at different locations. Although it provides the same amount of data as a single time series of 12 months, this scenario might present distinct challenges for ML forecasting. Figure 1 shows a TS with data collected at different frequencies or timesteps. For the TS with more frequent data collection (upper graph in Figure 1), identifying trends per watering cycle requires more complex ML models. Conversely, the TS with lower frequency but more irrigation cycles shows more visible trends.
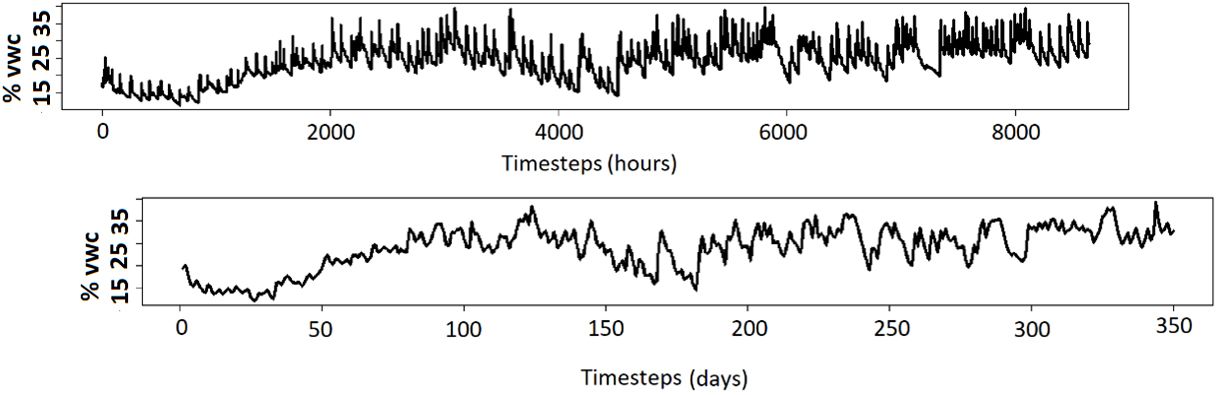
Credit: Eduart Murcia
- Machine learning algorithm complexity: Different ML algorithms have different data requirements. Some algorithms require more data to generalize effectively, while others can perform well with smaller data sets. Deep learning algorithms, such as recurrent neural networks (RNN) and convolutional neural networks (CNN), typically require larger data sets due to the number of parameters that need to be learned. However, they are capable of learning more complex structures. Simpler algorithms, such as decision trees, require less data but are usually limited to handling simpler data structures (Brownlee 2018; Brownlee 2022). Before selecting the ML algorithm, a review of published literature could initially guide the modeler to identify a set of appropriate algorithms for their study and its respective data requirements. Figure 2 shows a typical flowchart of the processes followed for ML training. These processes include data splitting (where an 80% to 20% training-to-testing ratio is commonly used), cross-validation, and benchmarking. Limited data can become an issue, especially for data splitting during ML training, validation, and testing. Insufficient data for validation can result in overfitting, where the model performs well on training data but fails to generalize to new data. Coming back to the example with the soil moisture sensors in the previous section, training the model with data collected hourly for only one month (i.e., three weeks of data for training and one week for testing) might be misleading.
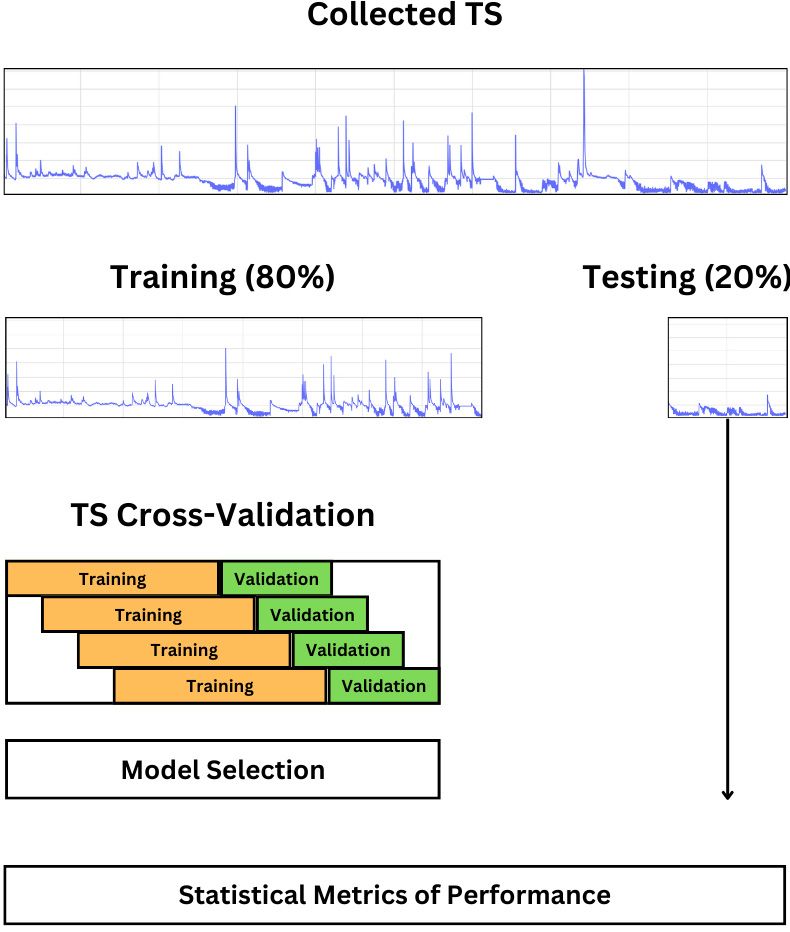
Credit: Eduart Murcia
Steps to Assess the Minimum TS Data Required
Standardizing the minimum number of data points is challenging. Follow the steps below to assess if the data collected is sufficient for an ML application.
- Using your expert scientific knowledge or getting assistance from an expert with relevant scientific expertise is the first step to assessing if the data is sufficient and representative. Making a graph and conducting an initial TS analysis can save time and enhance the quality of the ML forecast. A simple graph can reveal valuable data structure information, such as trends, seasonal cycles, and the signal-to-noise ratio. Figure 3 shows an example of the signal-to-noise ratio that a soil moisture sensor TS can contain. Simple noise-reduction techniques such as a moving average (iterative average calculation) or low-pass filters (setting cutoff limits to extreme values) are usually helpful. For more details on TS noise reduction, refer to Kostelich and Schreiber (1993) and Premanode et al. (2013). Ensure that the time series length encompasses several seasonal cycles and a noticeable trend shift. Figure 3 displays an example of a TS with multiple changes in seasonal patterns and long-term relationships (red line). In addition, autocorrelation function plots (ACF), used to identify correlations in TS, are easy-to-implement tools that better understand the TS data.* Figure 3 shows how general checks can be made using graphs. In this example, there are at least three short-term cycles in the TS (indicated by the green circle) after removing the noise components of the TS (represented by the blue line).
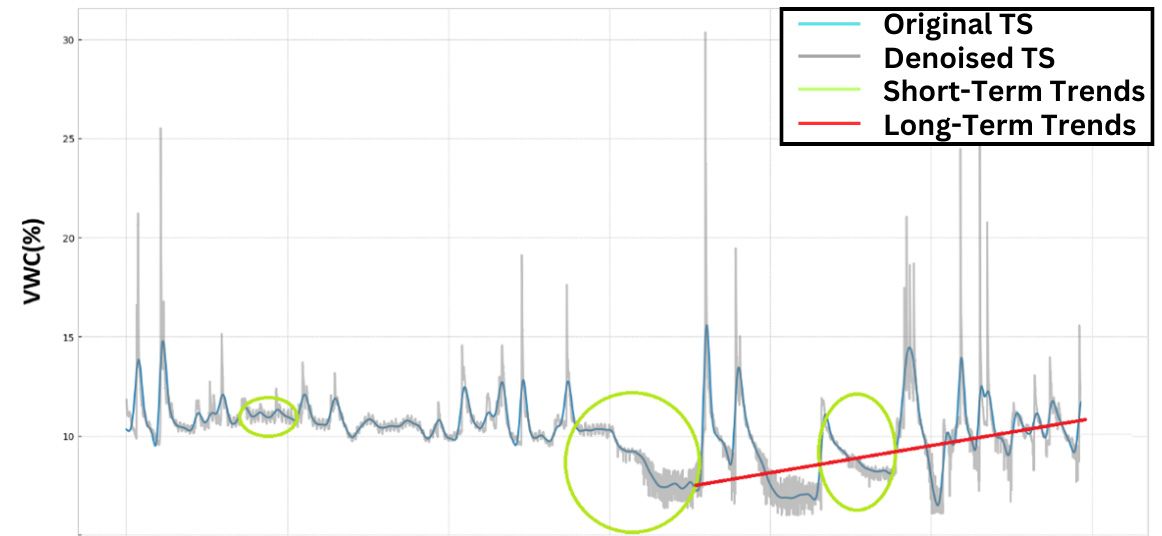
Credit: Eduart Murcia
2. Consider the length of the ML forecast or how far into the future the prediction is expected to be. The definition of short-term and long-term forecasting can vary significantly based on the context and the specific field to which it is applied. In hydrological applications, for instance, short-term forecasts could range from minutes to a few days in advance, while long-term predictions could range from months to years or decades (Jougla and Leconte 2022). Defining the expected time range of the forecast will contribute to understanding how many input data points could be relevant for the ML and how many training sets can be obtained given the length of past and forecast windows.
3. When there are few observations or limited data, classical statistical forecasting models, such as autoregression or autoregressive integrated moving average, could be an option. Classical statistical methods can outperform ML algorithms when few observations are available, and the nonlinearities of the TS are not dominant (Cerqueira et al. 2019).
4. Use heuristics (rules of thumb) only as a reference. For statistical algorithms, a preferable minimum number of observations is 100 for training (Box and Tiao 1975). ML algorithms require more data than statistical algorithms, so expect to factor this number for at least one order of magnitude.
Options to Increase the Size of the Time Series When Data Is a Limitation
Data augmentation techniques can be used to generate synthetic data to improve the quality and quantity of the data sets. The applicability of such approaches depends on the task type (forecasting or classification). Wen et al. (2021) present a comprehensive survey of data augmentation techniques for TS data classified according to the specific task. The techniques include adding noise (jittering), scaling the data, distorting the time intervals between samples (time-warping), and slicing the data. Implementing these techniques requires understanding all the statistical relationships such as mean, standard deviation (SD), autocorrelation, and the distribution of points over time to avoid altering the data (which would mislead the ML algorithm) or removing essential characteristics from the data. For instance, distorting the time intervals between samples might change the autocorrelation properties of the original time series (Um et al. 2017). Depending on the data set's characteristics and the research's purpose, this could mislead the ML forecast and the interpretations that can be made from it.
Case Study: Assessing Data Needs for Water Forecasting
In this example, the irrigation management team, consisting of a horticulturist, irrigation specialist, and data analysts, is interested in applying ML to forecast volumetric ion content (VIC) and soil water estimates for the next 24 hours for lettuce, sweet potato, and lemon irrigation. They have been collecting sensor data for four months and want to know whether this data would be enough to train an ML forecasting algorithm that could provide the team with sufficient time to respond to extreme weather events and manage their irrigation.
Data Conditions
Ten soil moisture sensors per crop measured volumetric water content (VWC) and VIC every 15 minutes. The sensors were installed four months ago at the beginning of the season. They have also been continuously collecting physiological data, including chlorophyll content and transpiration rate.
Lettuce
Using expert knowledge, the team horticulturist recommends at least two crop seasons because one lettuce season lasts between 30 and 70 days. In this case, the relationship between crop physiology and soil moisture content is a two-way interaction. The stage of the crop influences the water consumption rate, the soil structure, and the concentration of salts both in the root system and the soil. Thus, the team is confident that the available data would be sufficient to train an ML algorithm. They proceeded with graphing the data and performing an initial TS analysis and visual and statistical assessments of the data, and they found the data still seemed valid. With this quick analysis, they have decided that this data set is potentially usable with ML or deep learning algorithms. Meanwhile, they also recognize the importance of benchmarking the results from ML algorithms to guarantee that the proposed approach improves the current state of the art. Thus, they decided to include a list of algorithms to try a couple of statistical forecasting algorithms.
Sweet Potato
Using expert knowledge, the team concluded the data might not be enough, as one sweet potato season ranges between three to five months. However, they acknowledged the high frequency of data collection (15 minutes) that gives them around 11,500 data points per sensor. In this scenario, the data size could be worth trying (with the caveat that the complex models could tend to overfit). Thus, after using visual judgment and performing statistical analysis of the data, they decided not to discard the idea of using ML; however, they understood that they would have to limit the model's scope to represent primarily short- and middle-term variations. Also, they decided to use algorithms such as XGBOOST and Light-XGBOOST (Chen and Guestrin 2016). From a literature review, the team found evidence that these algorithms perform well in TS forecasting tasks without requiring massive data sets. They realized that testing the model's accuracy with unseen data would not be possible until additional data was collected. For this case, ML cannot be implemented; however, classical statistics might be an option.
Lemon
Using expert knowledge, the team concluded that the data is not enough because a lemon season can last three years after planting. Thus, the team decided not to use ML algorithms for their project. Although the option of data augmentation to generate synthetic data seems viable in this case, the team decided to collect at least one year of data to better understand the interaction between water management and physiological responses for this crop.
Concluding Remarks
ML algorithms are data-driven approaches whose performance highly depends on the amount of data available. However, data can often be limited in many projects. To obtain meaningful predictions, it is essential to consider multiple factors, including data granularity, complexity, and the complexity of the ML algorithm. This publication provides a set of steps for practitioners, researchers, and any scientist interested in developing projects using ML, particularly for TS data. This set of steps includes using expert knowledge, visual and statistical tools to characterize the TS, classical statistical approaches to benchmark the ML algorithms, and rules of thumb as a first filter to determine whether there is enough data. When data is a limitation, other approaches, including data augmentation, can be used as alternatives.
*There is a Python implementation of an ACF plot with an example that can be used for reference at https://github.com/SIHLAB/Data.
References
Brownlee, J. 2018. How to Develop a Skillful Machine Learning Time Series Forecasting Model. 1–16. https://machinelearningmastery.com/how-to-develop-a-skilful-time-series-forecasting-model/
Brownlee, J. 2020. Introduction to Time Series Forecasting with Python.
Brownlee, J. 2022. “How Much Data Is Required for Machine Learning?” Postindustria. https://postindustria.com/how-much-data-is-required-for-machine-learning/
Cerqueira, V., L. Torgo, and C. Soares. 2019. Machine Learning vs. Statistical Methods for Time Series Forecasting: Size Matters. http://arxiv.org/abs/1909.13316
Um, T. T., F. M. J. Pfister, D. Pichler, S. Endo, M. Lang, S. Hirche, U. Fietzek, and D. Kulic. 2017. “Data Augmentation of Wearable Sensor Data for Parkinson’s Disease Monitoring Using Convolutional Neural Networks.” ICMI ’17 - Proceedings of the 19th ACM International Conference on Multimodal Interaction: 216–220. https://doi.org/10.1145/3136755.3136817
Wen, Q., L. Sun, F. Yang, X. Song, J. Gao, X. Wang, and H. Xu. 2021. “Time Series Data Augmentation for Deep Learning: A Survey.” IJCAI International Joint Conference on Artificial Intelligence: 4653–4660. https://doi.org/10.24963/ijcai.2021/631