What Is the Value of an Existing Forest Stand?

The Land Expectation Value

The LEV for timber production (LEV) can be calculated using the following formula:

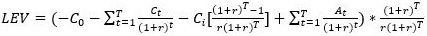
Where C₀ is the establishment costs¹ (site preparation and planting costs at stand age 0); C_t is the intermediate costs to grow the stand at time t (e.g., fertilization, marking, thinning costs); C_i is the annual management or administrative costs; A_t is the economic revenues due to thinning benefits and final harvest of the stand; and r is the discount rate.

Let's analyze the following example for a slash pine stand in Table 1. We assume that the slash pine is planted at year t=0 and harvested at age T=25 years. The slash pine is replanted immediately after harvesting. The costs and revenues associated with the activities indicated in Table 1 will remain identical for subsequent rotations².

Thus, the is determined as follows (Table 2):

The LEV approach is useful to determine the optimal decision when comparing two (or more) timber investments of unequal time frames (different rotation ages). The optimal decision, economically, is to choose the project with the highest land-expectation value (all projects assumed to be perpetual projects).

The Forest Value

The forest value is defined as the present value of cash flows arising from the land and the tree crop³. We previously defined that the LEV provides the present value of perpetual cash flows from identical rotations starting from bare land. This implies that the LEV remains unchanged. Thus, once a forest stand is already established, the value of the forest includes both the value of the land and the value of the timber. We can calculate the forest value of a mature stand that is ready for harvest or that of an immature stand with a harvest set for some point in the future.

Forest Value of a Mature Stand

The first case assumes that the stand is mature, i.e., it is ready to be harvested and regenerated immediately. Under this scenario, the forest value (FV) at time t can be expressed as:

FV_t = -C_t - C_i + A_t + LEV (Equation 2)

Equation (2) simply states that the forest value is the sum of the net value of the stand plus the value of the land. For example, let's consider a 20-year-old slash pine stand with a LEV = $947 per acre. At age 20 years, the intermediate costs C_t = 0 and management costs C_i = $20 per acre. In addition, the slash pine stand yields 28.1, 93.8, and 27.8 tons/acre of sawtimber, chip-and-saw, and pulpwood respectively. Thus, the value of timber A₂₀ = 27×28.1 + 19.9×93.8 + 10.4×27.8= $2,913 per acre. Thus, the forest value at time t = 20 is:

FV₂₀ = -20 + 2,913 (harvest revenues) + 947 = 3,840 per acre

Forest Value of an Immature Stand

The second case assumes that the stand is not ready to be harvested, and thus that the landowner will have to wait until time T to clear cut and replant a new forest stand. Assuming an n-year old stand (n = 1), the forest value FV can be defined as follows (Davis and Johnson 1987):

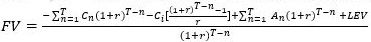
Equation 3 suggests that the forest value is the sum of future value of the remainder of the current rotation if the stand is harvested at age T plus the value of the land, discounted back T- n years. In this case, for a 20-year-old slash pine stand with an optimal rotation age of 25 years, the landowner only incurs management costs between ages 20 and 25 years. Furthermore, she/he receives the timber benefits at the moment of harvesting (25 years, $4,490 per acre). Thus, the forest value is:

FV₂₀ = [-20(1.055-1)/0.05+4,490+ 947]/(1.05)⁵ = $4,173 per acre

The FV formula also works as indicator to analyze forest management decisions. In our example, it suggests that it is economically convenient for the forest landowner to wait 5 more years to harvest the stand instead of harvesting the stand at age 20 years.

Conclusions

The land expectation value (LEV) formula is widely used to determine the profitability of a forest stand. It assumes that the land is bare of trees; thus, it does not consider the possibility of an existing forest stand. The forest value (FV) formula is a generalization of the LEV, including the value of the land and the value of the tree crop. The FV approach can be used to compare the value of the stand when it is immediately harvested or when it is economically immature. Thus, the FV formula can be used as a tool for valuing forest management options.

Notes

¹ We assume that the forest stand is artificially regenerated.

² Some silvicultural activities such as thinnings are carried out depending on the marketability of the removed trees, e.g., minimum tree-size specifications (length and diameter) have to be met. However, this type of constraint is not important for this publication because the main objective of this work is to illustrate, in a simple manner, how to determine the value of the forest stand.

³ The forest value can also incorporate nontimber benefits, for example, biodiversity, recreation, habitat, and water production.

References

Davis, L., K. Johnson. 1987. Forest Management. McGraw-Hill, NY. 790 p.

Faustmann, M. 1849. "Calculation of the value which forest land and immature stands Possess." Reprinted in Journal of Forest Economics (1995) 1(1): 89–114.

Hartman, R. 1976. "The harvesting decision when a standing forest has value." Economic Inquiry 14 (1): 52–55.

Pienaar, L. V., B. D. Shiver, and J. W. Rheney. 1996. Yield Prediction for Mechanically Site-Prepared Slash Pine Plantations in the Southeastern Coastal Plain. PMRC Technical Report 1996-3A, University of Georgia, Athens, GA.

Maggard, A., and R. Barlow. 2017. "2016 Costs and trends for southern forestry practices." Forest Landowner Magazine September/October, 31–39.

Timber Mart South, 2018. Us South Annual Review: 2018. University of Georgia Warnell School of Forestry and Natural Resources, Center for Forest Business, and Frank W. Norris Foundation, Athens, GA.