Introduction
By identifying audience subgroups, cluster analysis (a quantitative technique) helps Extension agents tailor their education and communication programs to specific audiences. This publication falls under the Cluster Analysis for Extension and Other Behavior Change Practitioners series and discusses key information and terminology associated with cluster analysis. The publication thus builds upon “Cluster Analysis for Extension and Other Behavior Change Practitioners: Introduction,” which introduced cluster analysis as a technique for audience segmentation. This publication provides essential information for the publications which follow, “A Practical Example” and “Integrating the Results of Cluster Analysis into Meaningful Audience Engagement.”
The purpose of this publication is to provide key terms and concepts needed to conduct this innovative audience research technique. The target audience for this document includes Extension professionals who want to use this technique and other social scientists working in any disciplinary area. Cluster analysis can be used to identify groupings of cases (i.e., people, respondents, or observations) or variables; this series focuses on how this technique can help identify the former.
There are many ways to conduct cluster analysis using a variety of disciplinary approaches and statistical software packages. One approach, audience segmentation, targets smaller subgroups that are likely to respond similarly to education and communications. (For more information, read the first publication in this series, “Cluster Analysis for Extension and Other Behavior Change Practitioners” or “Improving Extension Program Development Using Audience Segmentation.”) The information shared here is drawn from cluster analysis techniques used in social sciences—specifically from approaches applied to audience segmentation.
This publication would be most useful for application to continuous data (e.g., age, mean attitude scores, gallons of water saved as a result of a program). The options and definition presented below are aligned with SPSS software (Statistical Package for Social Sciences, IBM), although the concepts are more broadly applicable.
Cluster Analysis
Cluster analysis encompasses several “data reduction methods used for sorting cases, observations, or variables of a given dataset into homogeneous groups that differ from each other” (Yim & Ramdeen, 2015, p. 8). One of the assumptions of cluster analysis is that clusters exist (Qualtrics, n.d.). In other words, the methods assume that members of a target audience are different from one another (i.e., heterogenous). Cluster analysis can be used to reveal meaningful subgroups within a larger population. These insights can help professionals personalize education and communication programs, making them more relevant and effective for target audiences.
Cluster analysis can also be used to conduct audience research without bias because researchers do not apply judgment in subdividing groups beforehand (Qualtrics, n.d); when analyzing the clusters, researchers do not differentiate exploratory, dependent, and independent variables (Yim & Ramdeen, 2015). The variables that are input into statistical software and used to create clusters are called clustering variables. Once cluster analysis is conducted, analysts can treat the subgroup itself as an independent variable and other characteristics as dependent variables.
Sometimes the desired number of clusters is known (Sarstedt & Mooi, 2019). For example, one would need two clusters if they intend to find what distinguishes Extension service users from non-users. However, the ideal number of subgroups is typically not known, and cluster analysis techniques can be used to identify the ideal number of clusters and then assign individuals to those clusters. Hierarchical cluster analysis can suggest the ideal number of clusters that will maximize differences among groups, and k-means cluster analysis—a type of non-hierarchical cluster analysis—can be used to assign cases to a known number of groups. When the number of clusters is known beforehand, one can skip hierarchical cluster analysis and start with k-means analysis. These two primary types of cluster analysis are described below along with the terminology that supports running them. Sample size guidelines vary. Generally, the greater the number of clustering variables, the larger the sample size should be. One recommendation is 2X where x is the number of clustering variables (Sarstedt & Mooi, 2019); following this suggestion, if one has four clustering variables, they would need to analyze at least sixteen cases (24 = 16).
Hierarchical Cluster Analysis
Hierarchical cluster analysis is “a statistical technique where groups are sequentially created by systematically merging similar clusters together, as dictated by the distance and linkage measures chosen by the researcher” (Yim & Ramdeen, 2015, p. 8). This process is considered agglomerative and considers all cases as their own cluster at the start, thereafter “combin[ing] them until there is only one left” (IBM Corporation, 2021b) (Figure 1). This approach creates all possible numbers of solutions from a maximum of n (the total number of cases). Each case is assigned to its own single-case cluster (leftmost side of Figure 1); the cases are then reassigned to larger and larger clusters, until they all belong to a single cluster (rightmost side of Figure 1).
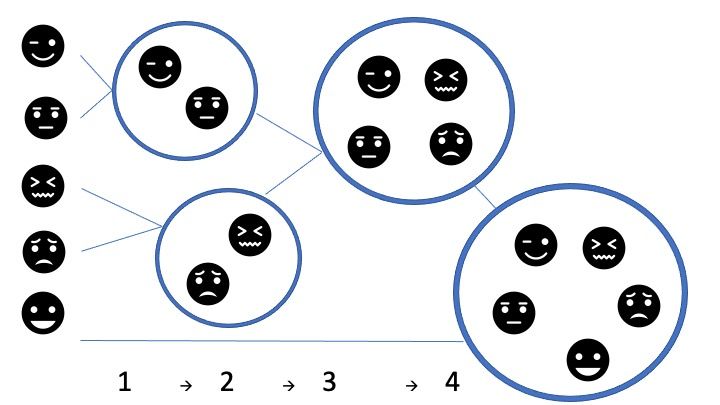
Credit: Laura A. Warner, UF/IFAS
Statistical software such as SPSS systematically combine the two most similar cases “into homogeneous clusters by merging them together one at a time in a series of sequential steps” (Yim & Ramdeen, 2015, p. 9; Gülağız & Şahin, 2017). Cases do not change cluster membership during hierarchical cluster analysis. At each step, the software either adds a new case to an existing cluster or considers the new case different enough from existing cluster(s) to form a new cluster. When using hierarchical clustering, the number of clusters is not decided beforehand.
While most hierarchical cluster analyses operate as described here, there is also a less common, divisive (in contrast to agglomerative) hierarchical cluster analysis method which operates in the reverse order: all cases are initially considered a single cluster (Yim & Ramdeen, 2015). Data standardization is recommended but not required for this analysis.
Hierarchical cluster analysis can be accessed from the SPSS menu by using:
Analyze > Classify > Hierarchical Cluster
A complete example with inputs and results is provided in the next publication in this series.
Two of the most important decisions to make when conducting hierarchical cluster analysis in SPSS regard the methods and distance measures, as discussed below. When conducting a cluster analysis in SPSS, there is an option to select Proximity Matrix as an output option; this matrix will present the distances specified below (Sarstedt & Mooi, 2019). There is also an option to produce an agglomeration schedule which visually depicts the clusters being combined at each stage of the process. The result of hierarchical cluster analysis is the number of clusters which will be used to run the subsequent cluster analysis.
Distance Measures
Distance measures are used to determine how similar or dissimilar single pairs of cases (or pairs of clusters that each contain only one case) are from one another so. These measurements, some of which are described below, allow the most similar cases to be placed in the same cluster (Gülağız & Şahin, 2017; Yim & Ramdeen, 2015):
- Euclidean distance is measured by the software as a straight line between variables (Sarstedt & Mooi, 2019).
- Squared Euclidean distance is the most common option for interval data (Statistics Solutions, 2022). This measurement uses an equation to calculate the total of squared differences between a pair of cases on the variables being compared, resulting in a single measure of overall distance (Yim & Ramdeen, 2015).
- Other distance measures for interval data include Pearson correlation, Cosine, Chebychev, Block, Minkowski, and a customized option.
- Other distance measures, such as matching coefficients or chi-squared measures, should be used when the data being explored are not continuous (Finch, 2005). (A discussion of these measurements is outside the scope of this document.)
At each step in the hierarchical cluster analysis procedure, the two cases with the shortest distance, according to the measure selected, are merged.
Hierarchical Cluster Method
In contrast to distance measures, which establish how similar or dissimilar single pairs of cases are from one another, linkage measures are used to determine how similar or dissimilar clusters (where at least one contains more than one case) are from one another (Qualtrics, n.d.; Yim & Ramdeen, 2015). Linkage measures, some of which are described below, are used to merge clusters with the shortest distance:
- The single linkage measure (also known as the nearest neighbor method) finds the shortest distance between any case in the first cluster and any case in the second cluster; after all clusters have been considered, the two clusters with the “nearest neighbors”/closest cases are combined (Sarstedt & Mooi, 2019; Yim & Ramdeen, 2015).
- The complete linkage method (also known as the furthest neighbor method), looks for the largest distance between any case in the first cluster with any case in the second cluster; after all clusters have been considered, the two clusters with the least “furthest neighbors”/furthest cases are combined (Yim & Ramdeen, 2015).
- The average linkage method considers the distance between two clusters as the average of the differences between each pair of cases from distinct clusters; this approach addresses some of the weaknesses of the previous two options (Yim & Ramdeen, 2015).
- Ward’s method calculates and squares the average similarity between each set of cases within a cluster relative to the sample as a whole (Sarstedt & Mooi, 2019). Cases are added to a cluster when their addition results in the smallest increase in this value.
- The centroid method first measures the distance between the average values of all variables in a potential cluster (Sarstedt & Mooi, 2019). (For more on centroids, see “Cluster Center” below.)
Other methods not discussed in this document include between-groups, within-groups, and median clustering.
Non-Hierarchical Cluster Analysis
Non-hierarchical cluster analysis is used to “first establish an initial set of cluster means and then assign each case to the closest cluster mean” (Yim & Ramdeen, 2015, p. 9). When using non-hierarchical clustering, the number of clusters is defined beforehand. In contrast to hierarchical cluster analysis, cases can change group membership during non-hierarchical cluster analysis. There are four specific types of non-hierarchical cluster analysis methods, and the k-means method is the simplest. K-mean cluster analysis is a technique which “first establish[es] an initial set of cluster means and then assign[s] each case to the closest cluster mean” (Yim & Ramdeen, 2015, p. 9) (Figure 2). The analysis assigns individual cases to specific clusters. After the software has run this analysis, the dataset gets a new variable; and each case is assigned its cluster number in the corresponding field.
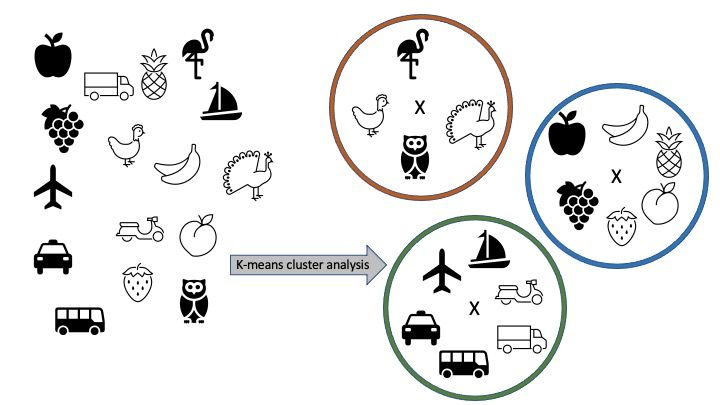
Credit: Laura A. Warner, UF/IFAS
K-means cluster analysis can be accessed from the SPSS menu by using:
Analyze > Classify > K-Means Cluster
Cluster Center
It is important to understand the concept of cluster centers when conducting k-means cluster analysis. Cluster centers, or centroids, are the average values of all the variables in a particular cluster (Sarstedt & Mooi, 2019). Each member of a specific cluster will be closer to its cluster center than that of any other cluster center.
k-means Cluster Method
When conducting k-means cluster analysis in SPSS, one must select a method. The two methods are updating cluster centers iteratively or classifying cases only. The former option takes a sample of some of the total cases to determine cluster centers, updating them through an iterative process until final cluster centers are determined and all cases are assigned to a cluster (IBM Corporation, 2021c). The “classify only” option only assigns cases to given, known cluster centers.
Summary
Though underused, cluster analysis techniques offer significant potential for guiding audience segmentation activities. These techniques can reveal natural groupings within the broader potential audience that may otherwise be unapparent. “Cluster Analysis for Extension and Other Behavior Change Practitioners: Introduction” introduced cluster analysis as a technique for segmenting an audience. This current publication defined some of the key terms and concepts one may need to know when conducting cluster analysis. This information would be most helpful in supporting a hierarchical cluster analysis (for identifying the appropriate number of clusters) followed by a non-hierarchical (k-means) cluster analysis (for assigning cases to those clusters) (Burns & Burns, 2008).
References
Burns, R. B., & Burns, R. A. (2008). Cluster analysis. In R. B. Burns & R. A. Burns (Eds.), Business research methods and statistics using SPSS (pp. 552–567). Sage.
Finch, H. (2005). Comparison of distance measures in cluster analysis with dichotomous data. Journal of Data Science, 3(1), 85–100. https://doi.org/10.6339/JDS.2005.03(1).192
Gülağız, F. K., & Şahin, S. (2017). Comparison of hierarchical and non-hierarchical clustering algorithms. International Journal of Computer Engineering and Information Technology, 9(1), 6–14. https://www.proquest.com/openview/f509f82f8d5184afd7b935efcadc0c3e
IBM Corporation. (2021a). Choosing a procedure for clustering. https://www.ibm.com/docs/en/spss-statistics/28.0.0?topic=features-choosing-procedure-clustering
IBM Corporation. (2021b). Hierarchical cluster analysis. https://www.ibm.com/docs/en/spss-statistics/28.0.0?topic=features-hierarchical-cluster-analysis
IBM Corporation. (2021c). K-means cluster analysis. https://www.ibm.com/docs/en/spss-statistics/28.0.0?topic=features-k-means-cluster-analysis
IBM Corporation. (2021d). TwoStep cluster analysis. https://www.ibm.com/docs/en/spss-statistics/25.0.0?topic=features-twostep-cluster-analysis
Qualtrics. (2023). What is cluster analysis? When should you use it for your survey results? https://www.qualtrics.com/experience-management/research/cluster-analysis/
Sarstedt, M., & Mooi, E. (2019). Cluster analysis. In A concise guide to market research. Springer texts in business and economics. Springer. https://doi.org/10.1007/978-3-662-56707-4_9
Statistics Solutions. (2022). Conduct and interpret a cluster analysis. https://www.statisticssolutions.com/free-resources/directory-of-statistical-analyses/cluster-analysis/
Warner, L. A. (2021). Cluster analysis for Extension and other behavior change practitioners: Introduction: WC399/AEC738, 11/2021.” EDIS, 2021(6). https://doi.org/10.32473/edis-wc399-2021
Yim, O., & Ramdeen, K. T. (2015). Hierarchical cluster analysis: Comparison of three linkage measures and application to psychological data. The Quantitative Methods for Psychology, 11(1), 8–21. https://doi.org/10.20982/tqmp.11.1.p008