Irrigation systems can be used to deliver soluble chemicals to the crop. Depending on the type of irrigation system, chemicals may be applied to the root zone, the aerial part of the plant, or both. The process of chemical transport using the irrigation system is referred to as chemigation (Bayabil et al., 2020a). Specific terms, such as nematigation and fertigation, may be used to refer to specialized applications of chemigation.
Irrigation systems designed or adapted for chemigation require specialized equipment for the injection of the chemical solution into the irrigation system at a controlled rate. Several injection methods are possible and are discussed in detail in other publications (Nakayama and Bucks, 1986; Smajstrla et al., 1987; and Yeager and Henley, 1987). The cost, accuracy, reliability, and longevity of the equipment varies greatly among manufacturers.
It is important to select adequate equipment, maintain it regularly, and properly operate it to insure a successful chemigation system. New irrigation system designs must consider which chemicals are to be injected while selecting the system components to insure compatibility. The uniformity of chemical application cannot exceed that of the irrigation system. Therefore, it is very important to have a well-designed and well-maintained irrigation system to provide the greatest potential for a high level of application uniformity (Bayabil et al., 2020b). When existing irrigation systems are to be adapted for chemigation, they should be thoroughly examined for uniformity of application as well as compatibility of the chemicals to be injected with existing components.
Water quality is another factor to consider in the design or adaptation of an irrigation system for chemigation. Some water supplies require chemical amendment to prevent bacterial growths or chemical precipitants from clogging the system. This publication will concentrate on the management aspects of chemigation and how chemigation influences other aspects of irrigation management.
Chemical Mixtures and Injections
Chemicals may be applied as a precisely managed level of concentration or as a bulk mass of chemical with possibly varying concentration levels. Concentration management requires a precise injection system and is more involved than bulk injection. The injection system must be specifically calibrated for the irrigation system it is to be operated on and under the operating conditions that will exist when chemicals are to be injected. Variations in operating pressure, system flow rate, and, at times, even temperature can influence the calibration of the system. Bulk injection simply involves the injection of a desired volume or amount of chemical into the system. The injection rate does not need to be precisely controlled. However, it should not be damaging to any part of the system or crop, should not exceed manufacturers' recommended application rates, and should apply the chemical in a time period which does not result in over-irrigation or leaching of previously applied chemicals.
Concentration Mixtures of a Stock Solution
Some chemical applications require that a certain concentration level be maintained for proper use of that chemical in that situation. Concentrations are generally expressed in parts per million (ppm), which is not a convenient term for mixing purposes. Chemicals may be supplied in dry form or liquid form; however, the end result is a liquid mixture of a desired concentration. The following equation can be used to determine the mass of chemical required to achieve a particular ppm level. (Equation 1)
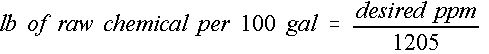
Credit: undefined
This provides the mass of actual chemical that must be dissolved per 100 gallons of water. For example, a 200 ppm concentration level of nitrogen as a fertilizer solution will require, as shown in Equation 2:
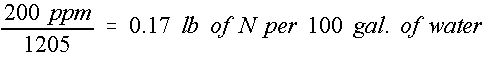
Credit: undefined
This is pounds of actual nitrogen required and not pounds of fertilizer mix as either a dry or liquid source.
Many chemicals are supplied as either a percentage by weight of a dry or liquid mixture. Therefore, the mass of chemical mixture required will depend on the concentration of raw chemical in the mixture. Equation 3 can be used to determine the mass of chemical mixture required to provide the necessary level of raw chemical.

Credit: undefined
where
M(mixture)=the required mass of chemical mixture (lb.),
M x =the desired mass of chemical X (lb.), and
%X=the percentage of chemical X in the mixture.
If, in the above example, a 16-4-8 (N-P 2 O 5 -K 2 O) dry fertilizer mix was used, then the required mass of fertilizer mix for 100 gallons of solution is shown in Equation 4:
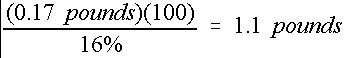
Credit: undefined
Therefore, 1. 1 pounds of 16-4-8 fertilizer source mix are required to supply 0.17 pounds of nitrogen.
Table 1 combines both Equations (1) and (3) to provide the mass of chemical mixture (for example, fertilizer mix) to add to 100 gallons of water to obtain a certain ppm level for the desired chemical. An example using Table 1 is included in the Appendix.
It is important to remember that the A-B-C analysis of a fertilizer label refers to the nitrogen (N), phosphorus oxide (P 2 O 5 ), and potash (K 2 O). Therefore, only 44% of the B factor (P 2 O 5 ) refers to actual phosphorous (P), and only 83% of the C factor (K 2 0) refers to actual potassium (K). Equation (3) can be slightly rearranged to solve for M x based on M(mixture) and used to determine the mass of actual P or K contained in a fertilizer mix. For example, in 50 pounds of 16-4-8 fertilizer, the mass of P 2 O 5 is shown in Equation 5:
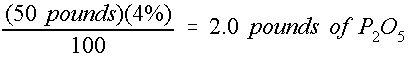
Credit: undefined
Similarly, the mass of actual P is shown in Equation 6:
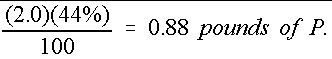
Credit: undefined
Therefore, 50 pounds of a 16-4-8 fertilizer mixture contains only 0.88 pounds of actual P. The same procedure can be used to determine that the amount of actual K is 3.32 lbs.
When chemicals are supplied in liquid form, it is more convenient to measure volumes rather than masses or weights. This requires the specific density or specific weight (S x ) of the liquid mixture, such as pounds of chemical per gallon of liquid. This property should be provided by the manufacturer or chemical supplier and can be used to simply convert from required lbs. to required gallons. For example, a liquid fertilizer provided as a 4-0-8 solution has 4% nitrogen by weight. However, the amount of nitrogen is not known unless the specific weight of the chemical (fertilizer) solution is known, such as 9.6 lb. per gallon. As was previously mentioned, this value varies among chemical mixtures and should be on the chemical label but may be obtained from the chemical supplier.
Concentration Injection Rates
The previous section described the procedure for mixing particular concentrations of a stock solution. However, many systems will have flowing water with a requirement to maintain a desired concentration of a chemical in that system. This requires injecting a supply mixture at the proper rate to maintain the desired concentration level. The following equation or Tables 2 and 3 can be used to determine the injection rate necessary to maintain the desired concentration of a chemical X. (Equation 7)
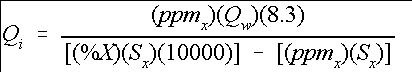
Credit: undefined
where
Q i =Injection rate in gallons per minute (gpm),
Q w =Water supply flow rate (gpm),
8.3=Specific weight of water (lb./gal.),
ppm x =Desired ppm level of chemical X,
%X=Percentage of chemical X in the stock solution, and
S x =Specific weight of the stock solution mix (lb. /gal.).
For example, chlorine is to be injected to provide 10 ppm of free chlorine into a micro-irrigation system, which has a system flow rate of 550 gpm. (Equation 8) The chlorine stock solution contains 5% free chlorine (sodium hypochlorite source, NaOCl) and has a specific weight of 9.1 lbs. per gallon. Therefore,
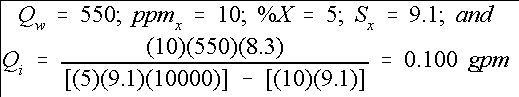
Credit: undefined
Therefore, the injector should be set to provide 0.10 gallons per minute of stock solution into the irrigation system in order to maintain an injected free chlorine level of 10 ppm. The actual ppm of free chlorine throughout the system will depend on how much free chlorine is used by organics in the water supply and in the irrigation system.
If the specific weight of the chemical is close to that of water, Equation (7) can be simplified. The simplified approximation to Equation (7) is shown in Equation 9:
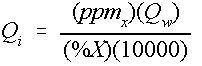
Credit: undefined
where
Q i = Injection rate in gallons per minute (gpm),
Q w = Water supply flow rate (gpm),
ppm x = Desired ppm level of chemical X, and
%X = Percentage of chemical X in the stock solution.
In repeating the above chlorine example, we get as shown in Equation 10:
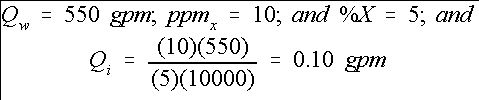
Credit: undefined
This result is consistent with the previous example. In most cases, Equation (9) may be used. However, if greater accuracy is needed, then use Equation (7). Some injectors are operated to inject on a gallons-per-hour (gph) basis. Therefore, the injector rate determined above must be converted using Equation 11:
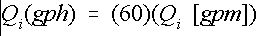
Credit: undefined
For example, a flow rate of 0.10 gpm is equal to a flow rate of 6.0 gph.
Injection Volumes and Periods
Chemical mixtures may be injected directly from the stock supply tank or from an injector feeder tank. Injector feeder tanks are useful for injecting a specific volume of liquid, regardless of the injection rate. When the tank is empty the desired volume of chemical mixture has been injected. This procedure eliminates excess applications of chemicals which may occur due to pump or controller failure.
The size of the required feeder tank will depend on the volume of chemical mixture to be injected, which in turn will depend on either the total amount or volume of chemical to be applied or on the length of the injection period. Volumetric applications can be based on area applications or the sum of individual applications. For example, a pesticide may require that X pounds of a chemical be applied per acre; a vegetable grower may want to apply a certain mass of fertilizer per acre or per 1000 bedded feet of plant row; or a citrus or nursery operator may want to supply a certain amount of fertilizer per irrigated plant. In addition to the desired level of fertilization, these situations require knowledge of the irrigated acreage per set, total feet of bedded production area irrigated per set, or the number of plants or trees irrigated in each set.
Summary
Information pertaining to the injection of chemicals into irrigation systems was discussed in terms of concentration injections, bulk injections, quantity of chemicals to be injected, injection system calibration, and injection periods. The information was provided to assist irrigation system designers and operators with the chemigation aspects of irrigation system design, scheduling, and management.
Table Examples
- How much 10-10-10 soluble fertilizer mix is required to mix with water to make a 100 ppm solution of actual nitrogen? From Table 1, a value of 0.83 lb of soluble fertilizer is required per 100 gallons of water (solution) to provide a 100 ppm solution of nitrogen.
- Chlorine is to be injected into an irrigation system which has a water delivery (supply) rate of 400 gpm. The chlorine stock solution contains 8% of "free" chlorine. What stock solution injection rate is necessary to provide 20 ppm of "free" chlorine to the irrigation supply water? Table 2 (or Table 3 ) indicates that to provide a 20 ppm concentration level with an 8% stock solution, approximately 0.025 gpm (1.50 gph) of stock solution injection is necessary per 100 gpm of water delivery rate. Therefore, a 400 gpm water delivery rate requires a stock solution injection rate of:
(0.025 gpm/100 gpm) (400 gpm) = 0.10 gpm .
or
(1.50 gph/100 gpm)(400 gpm) = 6.0 gph.
Therefore, injecting an 8% stock solution of chlorine at 0.10 gpm (6.0 gph) into an irrigation system with a system flow rate of 400 gpm will provide approximately 20 ppm of "free" chlorine into the system.
3. A vegetable field is to be fertigated (have fertilizer injected) on a weekly basis with three pounds of nitrogen (N) per 1000 feet of plant bed per week. The field is 25 acres in area with 6000 bedded feet per acre. What size of feeder tank is necessary to hold the required volume of fertilizer mixture if the mixture is a 4-0-8 solution with a specific weight of 10 lb/gal?
The required amount of fertilizer is:
=(3 lb/1000 ft) (6000 ft/acre) = 18 lb/acre
=(18 lb/acre) (25 acres)
= 450 lb of N per week.
Table 4 is used to determine the amount of chemical (nitrogen) per gallon of solution. A 4-0-8 solution of fertilizer (S x = 10) has 4% nitrogen.
From Table 4, read the actual amount of N as 0.40 lb per gallon of solution.
Next use Table 5 to determine the required volume of mixture. For a 0.40 lb/gal chemical (nitrogen) density and 450 lb requirement, read 1125 gallons of fertilizer mixture required. Therefore, the supply tank must have a minimum capacity of 1125 gallons to hold the weekly supply of fertilizer.
References
Bayabil, H.K., K.W. Migliaccio, J.H. Crane, T. Olczyk, and Q. Wang. 2020a. Regulations and Guidelines for Chemigation. University of Florida IFAS Extension. Publication AE542/AE542. 2020/4: https://edis.ifas.ufl.edu/publication/AE542
Bayabil, H.K., K.W. Migliaccio, M.D. Dukes, and L. Vasquez. 2020b. Basic Tips for Designing Efficient Irrigation Systems. University of Florida IFAS Extension. Publication #AE539. 2020/1: https://doi.org/10.32473/edis-ae539-2020
Clark, Gary A., Dorota Z. Haman, and F. S. Zazueta. (1996) 1998. “Injection of Chemicals Into Irrigation Systems: Rates, Volumes, and Injection Periods: BUL250/AE116, 10/1998”. EDIS 1998 (October). Gainesville, FL. https://doi.org/10.32473/edis-ae116-1996.
Nakayama, F.S., and D.A. Bucks. 1986. Trickle Irrigation for Crop Production: Design, Operation, and Management. Elsevier. Amsterdam. 383 p.
Smajstrla, A.G., D.S. Harrison, W.J. Becker, F.S. Zazueta, and D.Z. Haman. 1985. Backflow Prevention Requirements for Florida Irrigation Systems. Bulletin 217. Gainesville: University of Florida Institute of Food and Agricultural Sciences. https://original-ufdc.uflib.ufl.edu/UF00008439/00001/1000
Haman D.Z., and F.S. Zazueta. 1986. Chemical Injection Methods for Irrigation. (revised). Gainesville: University of Florida Institute of Food and Agricultural Sciences. https://edis.ifas.ufl.edu/publication/WI004
Hochmuth G. J. Fertilizer Management for Greenhouse Vegetables—Florida Greenhouse Vegetable Production Handbook, Vol 3. https://edis.ifas.ufl.edu/publication/CV265
Table 1. The mass (lb) of chemical mixture (i.e., fertilizer mix) to add to 100 gallons of water for different ppm level solutions.
Table 2. Chemical injection rate expressed in gpm of injection rate per 100 gpm of irrigation system flow rate for different desired concentration levels (ppm) and different stock solution concentration levels.1
Table 3. Chemical injection rate expressed in gph of injection rate per 100 gpm of irrigation system flow rate for different desired concentration levels (ppm) and different stock solution concentration levels.1
Table 4. The mass (lb) of active chemical contained per gallon of stock solution (Smx) for different combinations of specific weight and chemical concentration.
Table 5. Required volume (gal) of chemical mixture to provide a desired level of an active chemical for different concentrations (lb/gal) of the chemical in the stock solution from Table 4.