Introduction
Investment decisions are among the most important management decisions farmers make. In many cases, those investments are in capital assets such as establishing a new orchard or purchasing a new piece of equipment. Investments in capital assets typically involve different timings for expenses and returns (cash flows), with one large investment at the beginning of the investment period and multiple returns spread over the remaining lifetime of the asset. The process for evaluating those investments is called investment analysis or capital budgeting. The objective of this article is to review the two main criteria for decision making when evaluating whether to invest in a capital asset, namely, the net present value (NPV) and the internal rate of return.
The Time Value of Money
People intuitively recognize that the value of a dollar today is greater than the value of a dollar next year (or any other time in the future). This is so because anyone with a dollar today could invest it and receive more than a dollar next year (one dollar plus interest). Therefore, interest illustrates the relationship between two amounts of money at different moments in time; it denotes the concept of the time value of money.
There are other factors that also justify (paying or receiving) interest. Inflation refers to the overall increase in the price of goods and services over time. Thus, inflation decreases the purchasing power of money because consumers will not be able to purchase the same amount of goods and services with, say, $100 next year compared to what they can buy today. Risk is another factor that makes people prefer receiving one dollar today rather than next year; an unforeseen circumstance during the forthcoming year might make it impossible to receive that dollar in the future. Therefore, a proper capital investment analysis should take inflation and risk into account.
Discounting and Present Value
Present value refers to today's value of an amount of money that will be received or paid in the future. Discounting is the process of finding such present value by using an interest rate (also called discount rate). The following formula illustrates the relationship among the variables:
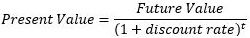
where t denotes the number of time periods in the future. For example, assuming a discount rate of 10%, the present value of $110 next year can be obtained by plugging in the values in the formula above:
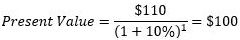
Using instead a discount rate of 5% would make the present value (rounding to the nearest dollar) be $105. Thus, the discount rate plays a key role in the discounting process. Figure 1 illustrates the relationship between discount rates and the present value; the higher the discount rate, the lower the present value. Thus, a key consideration for any grower performing an investment analysis is what discount rate to use. If a grower needs to borrow money to finance an investment, say at 10%, then that would be an appropriate rate to use in the calculations. However, if instead a grower were to use his own savings, which (for example) may obtain a 4% interest rate in an alternative investment, then that should be the discount rate used in the analysis. If not already factored in, the inflation rate should also be added to obtain the appropriate discount rate.
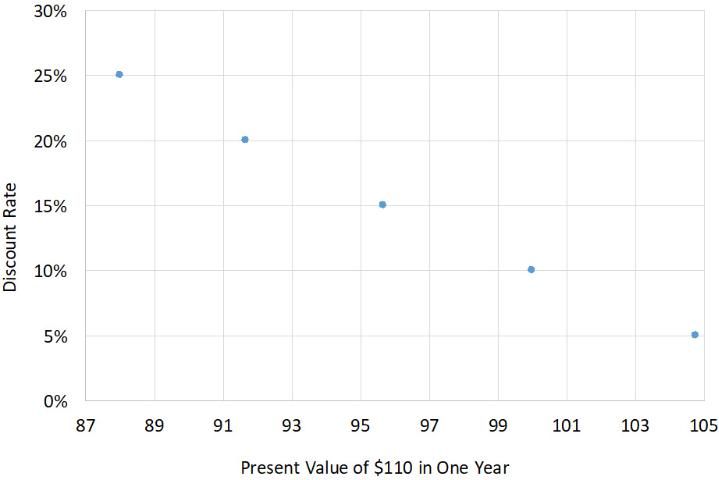
In addition, the presence of risk also justifies paying or receiving interest. Thus, when making calculations for investment analysis, growers should incorporate a risk premium to the discount rate. This is so because the greater the risk, the greater the return a grower would expect to obtain to be willing to take the risk. The amount of risk premium, however, is subjective. This is because different growers might rate the same investment as having a different level of risk. In addition, it is important to realize that by adding a risk premium to the discount rate, the grower is requiring that the net cash revenue of the investment be higher. Thus, the discount rate can then be interpreted as the minimum rate of return required for the investment to be attractive to the grower (Kay, Edwards, and Duffy 2012).
Methods for Evaluating Investment Analysis
The Net Present Value (NPV) is the most popular method for evaluating investments in capital assets. It consists in summing the present value of the different cash flows throughout the life of the investment and subtracting the initial investment. Thus, the formula for NPV can be written as follows:
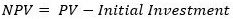
Assuming we are evaluating an investment with a useful life of 10 years and the relevant discount rate is 10%, the formula for computing the NPV is as follows:
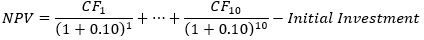
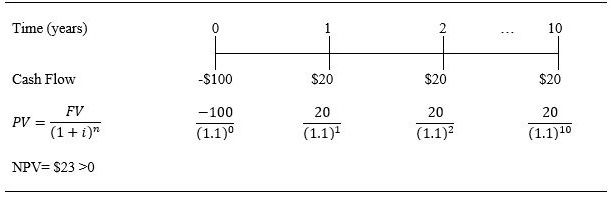
Figure 2 illustrates an example in which the initial investment at time zero is $100, and in each of the following 10 years a cash flow of $20 is obtained. As a rule of thumb, investments with a positive NPV should be accepted and those with a negative NPV, rejected. The rationale for accepting investments with positive NPVs is that they yield higher returns than the discount rate (cost of capital). The example in figure 2 yields a NPV of $23, so the investment should be accepted.
The Internal Rate of Return (IRR) is an alternative method for evaluating whether to undertake a capital investment. The IRR is the discount rate that makes the NPV of an investment be zero. The following formula illustrates how the IRR is calculated continuing with the example above:
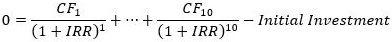
The major advantage of the IRR methodology is that it does not require the grower to determine what discount rate to use because the Internal Rate of Return is intrinsic to the investment that is being analyzed (Ross, Westerfield, and Jaffe 2005).
To illustrate the concepts discussed above, consider an investment in a one-acre blueberry orchard in Florida as described by Singerman et al. (2016). Table 1 shows the costs, revenues, annual cash flows, accumulated cash flow, and present value of cash flows from investing in a blueberry orchard with a 10-year lifetime. The cost in year 0 refers to the estimated establishment costs or initial investment, whereas the costs in years 1 through 10 refer to the estimated annual maintenance costs. Revenue in the first two years is zero because the plants start bearing fruit in year 3.
As shown in Table 1, the NPV is positive using discount rates of 5 and 10%. Thus, if any of those interest rates represent the grower's cost of capital, the grower should go ahead and establish the blueberry orchard. However, if the grower's cost of capital is 15%, the NPV becomes negative and the grower should not invest in the blueberry orchard. As also shown in table 1, the IRR of investing in one acre of blueberries yields a return of 12.3%, which also helps explain why the result of the NPV is positive using a 10% discount rate but it is negative when using a 15% interest rate; the discount rate that makes the NPV zero is between those two.
Summary
Paying or receiving interest illustrates the concept of the time value of money. Therefore, the interest rate is a key element to take into account when evaluating investments in capital assets because they involve cash flows at different moments in time. The two major methodologies for evaluating capital assets that incorporate the time value of money are the NPV and IRR. A positive NPV denotes that the revenue cash flows from an investment are higher than the cost cash flows. When the IRR of an investment is higher than the cost of capital, it denotes the investment is profitable.
References
Kay, R. D., W.M. Edwards, and P.A. Duffy, 2012. Farm management, 7th ed. McGraw-Hill, New York, NY.
Ross, S. A., R.W. Westerfield, and J. Jaffe. 2005. Corporate Finance, 7th ed. McGraw-Hill/Irwin, New York, NY
Singerman, A., M. Burani-Arouca, J. G. Williamson, and G. K. England. 2016. Establishment and Production Costs for Southern Highbush Blueberry Orchards in Florida: Enterprise Budget and Profitability Analysis. FE1002. Gainesville: University of Florida Institute of Food and Agricultural Sciences. https://edis.ifas.ufl.edu/publication/fe1002